Дан правильный шестиугольник ABCDEF. Найдите AB. Если BF=корень из 75

Решение:

Пусть АВ=х

ВF=корень из75

ВF пересекает АД в т. О.

ВО=ОF=(корень из75)/2

угол А = 120 градусов

треугольник АВF равнобедренный, углы при основании =(180=120):2=30

катет, лежащий против угла 30 градусов = половине гипотенузы =>

в треугольнике АВО:

х^2=(х/2)^2+((корень из 75)/2)^2

х^2=х^2/4+75/4

4х^2-х^2=75

3х^2=75

х^2=25

х=5

Ответ: АВ=5см.

Дан правильный шестиугольник ABCDEF. Найдите BD, если AB= корень из 3

Так как шестиугольник правильный, значит все его стороны равны, АВ=BC=CD  и тд, Проведем диагонали. См рис

OC=BC=OB, потому что ромб был правильный, и мы получили правильные треугольники

Нам надо найти большую диагональ ромба, мы знаем, что диагонали ромба пересекаются под прямым углом( угол  B01C=90) и делятся точкой пересечения пополам.

значит OO1=OC/2= sqrt 3/2

по теореме Пифагора найдем  OO1

ВO1= sqrt (ОО1^2 + OB^2) = sqrt(3/4+ 3) = sqrt 15/4=5/2

BD=2BO1= 2*5/2=5

ответ 5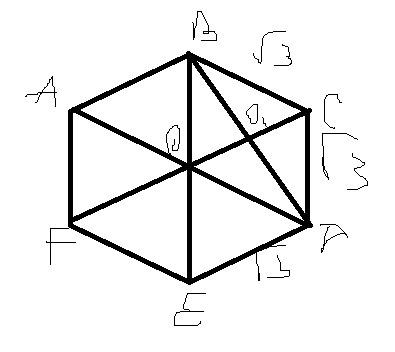