Сколько сторон у правильного многоугольника, внешний угол которого равен шестидесяти градусам?


Главная Научный калькулятор
Меню Алгебра Геометрия Основные понятия Аксиомы планиметрии Углы Перпендикулярные и параллельные прямые Перпендикуляр и наклонная Круг (окружность) Треугольник Четырехугольник Параллелограмм Трапеция Многоугольники Основные понятия стереометрии Аксиомы стереометрии Прямые в пространстве Пересекающиеся прямые Параллельные прямые Скрещивающиеся прямые Прямая и плоскость в пространстве Перпендикулярность прямой и плоскости Параллельность прямой и плоскости Угол между прямой и плоскостью Теорема о трех перпендикулярах Формула двойного проектирования Плоскости в пространстве Пересекающиеся плоскости Параллельность плоскостей Перпендикулярность плоскостей Площадь проекции плоской фигуры на плоскость Многогранники: Пирамида Призма Тела вращения: Цилиндр Конус Шар (Сфера) Объем тел вращения Задачи по геометрии Примеры решений Вспомогательные материалы: Таблицы Брадиса Исследование функций Асимптоты. Первая производная. Вторая производная. Графики функций Задачи по функциям Тригонометрия Тригонометрические неравенства	Треугольник : Равнобедренный треугольник : Прямоугольный треугольник : Четырехугольник : Параллелограмм : Ромб : Прямоугольник : Трапеция : Многоугольники : Круг и окружность : Прямые и плоскости : Пирамида : Системы координат : Цилиндр : Конус : Углы : Призма : Параллелепипед : Сфера и Шар : Построения Сколько сторон у правильного многоугольника, внешний угол которого равен шестидесяти градусам? Решение: Сумма всех внешних углов любого многоугольника =360 градусов. Если многоугольник правильный, то все внешние (и внутренние) углы равны между собой. Значит, 360:60=6. Будет правильный шестиугольник. А формула 180(n-2) - это сумма внутренних, а не внешних, углов многоугольника. Кстати, если пользоваться этой формулой, то получим так. Внутренний угол многоугольника будет 180-60=120. Количество углов в правильном многоугольнике= колич. Его сторон = n. 180(n-2)=120n 180n-360=120n 60n=360 n=6 Получили то же самое. Сколько сторон имеет многоугольник, если число всех его диагоналей в 2,5 раза больше числа его сторон Как известно количество вершин и сторон в любом многоугольнике совпадает, пускай в нашем случае их будет х, дальше будем рассуждать следующим образом: чтобы узнать число диагоналей каждую вершину соединяем с другими вершинами, кроме нее самой и соседних, получаем х (х-3), но так как при таком соединении диагонали повторяются 2 раза, то их число в х-угольнике будет х(х-3)/2 по условию имеем соотношение (х(х-3)/2)/х = 2,5 х² - 3х = 5х х² - 8х = 0 х = 0 либо х = 8 первый корень не удовлетворяет условию, значит х = 8 Ответ: 8 Сколько сторон имеет многоугольник, если каждый его угол равен 177 Сумма внешних углов выпуклого многоугольника, взятых по одному при каждой вершине, не зависит от n и равна 360°, где n – число сторон n-угольника. Если на каждой стороне многоугольника построить равнобедренный треугольник, то величина угла при вершине будет равна 3°, а сумма этих вершин 360°. Угол при вершине - 180-177=3°. Количество углов - 360/3=120. Количество сторон равно количеству углов - 120 сторон. Соотношение площадей вписанной и описанной окружностей =0,75. Периметр правильного многоугольника 12см. Сколько сторон имеет многоугольник и каковы радиусы окружностей. 1. По условию S₁/S₂ = 0,75 => r²/R² = 0,75 r - радиус вписанной окружности R - радиус описанной окружности r² = 0,75R² 2. 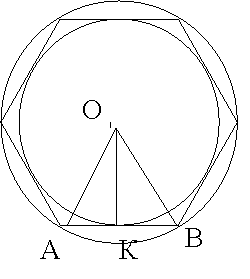ΔАОВ - один из секторных треугольников данного многоугольника B ΔAOB AO = BO = R OK ⊥AB OK = r В прямоугольном ΔAOK по теореме Пифагора AK² = AO² - OK² AK² = R² - r² AK² = R² - 0,75R² AK² = 0,25R² √AK² = √(0,25R²) AK = 0,5 R это значит, что катет АК равен половине гипотенузы АО, т. Е R Следовательно, < AOB = 60° ΔAOB - равносторонний n = 360° : 60° = 6 n = 6 - это означает, что это шестиугольник 3. P = 12 cм a = 12 : 6 = 2 см - сторона a = R = 2 cм r = √(0,75R²) = R/2√3 *r = 2/2 √3 = √3 ≈ 1,7 cм Ответ: шестиугольник n = 6; R = 2 cм r = √3 ≈1,7 cm Радиус окружности, описанной около правильного многоугольника, равен 6√3 см, а радиус вписанной в него окружности - 9 см. Сколько сторон имеет многоугольник? Так как многоугольник правильный ⇒ центры вписанной и описанной окружности общее, обозначим центр буквой О. Берем произвольный сектор АОВ; С точка касания вписанной окружности с АВ ⇒ R = OA = 6√3 ; r = OC = 9 OC : OA = r : R = Cos(∠AOC) Cos(∠AOC) = 9 : 6√3 = √3/2 ⇒ ∠AOC = 30° ⇒ ∠AOB = 60° = 1/6 · 360° ⇒ Многоугольник - шестиугольник. Ответ 6 Сколько сторон имеет выпуклый многоугольник с суммой углов 2160 градусов Сумма углов выпуклого многоугольника находится по формуле: N=180°• (n – 2), где N - сумма углов, n - их количество ( а, значит, и число сторон многоугольника). Но известно, что сумма внешних углов выпуклого многоугольника равна 360°, причем, с каждым внутренним углом внешний составит в сумме развернутый угол, т.е. 180°. Очевидно, что сумма всех внутренних и внешних углов кратна числу 180°. Тогда число сторон данного выпуклого многоугольника (2160°+360°):180°=14 - Теперь вычислим то же число по формуле: 2160°=180°• (n – 2), 2160°=180°•n-360 180°•n=2160°+360°⇒ n=2520°:180°=14 (сторон) Сумма всех внутренних углов выпуклого многоугольника с одним из его внешних углов равна 1000º. Сколько сторон у этого многоугольника? Число сторон равно 7. Рисунок здесь без надобности. Сумма всех внутренних углов выпуклого многоугольника 180º•(n-2), где n- число сторон. Сумма всех внешних углов выпуклого многоугольника 360º. Допустим, что многоугольник правильный. Тогда каждый внешний угол будет 360º:n Заданную сумму всех внутренних углов правильного многоугольника с одним из внешних можно выразить уравнением: 180º•(n-2)+360º:n=1000º 180n²-360n+360=1000n⇒ после несложных преобразований получим 9n²-68n+18=0 Корнями этого квадратного уравнения ≈7,3 и ≈0.3; Количество сторон многоугольника не может быть дробным и не может быть меньше трех**. Зато градусная мера его углов может быть выражена не целыми числами. Многоугольник по условию не задан правильным. Следовательно, количество его сторон может быть равно семи. Проверим: 180•(7-2)+x=1000º х=1000º-900º=100º Подходит. - Сумма внутренних углов восьмиугольника больше 1000º - следовательно, сторон меньше 8. Сумма внутренних углов шестиугольника 720º. Тогда внешний угол должен быть 1000º-720º=280º, чего быть не может. Внешний угол со смежным внутренним в сумме составляют развернутый угол, т.е. 180º. Ответ: Число сторон данного выпуклого многоугольника 7.