Даны две точки А(-5; 3) и В(3; 5). Докажите, что точка В может быть получена из точки А поворотом вокруг начала координат на 90по часовой стрелке.

Решение:

Рисуем точки на осях. От точки А опускаем перпендикуляр к оси х и называем точку пересечения D, от точки B опускаем перпендикуляр к оси y и называем точку пересечения C.

AD=BC=3, DO=CO=5, угол ADO=BCO=90, значит треугольники ADO и BCO равны, а значит равны и их гипотенузы AO и BО.

Угол DAO=AOC, так как оба получены вследствие пересечения параллельных прямых AD и СО прямой АО. Так как треугольники равны, значит угол DAO=CBO.

Угол AOB = AOC+COB = DAO+COB=CBO+COB

В треугольнике COB угол OCB прямой, значит сумма двух оставшихся углов = 180-90=90

Значит CBO+COB=90 градусов.

Значит, если повернуть точку B на 90 градусов против часовой стрелки, получим точку A.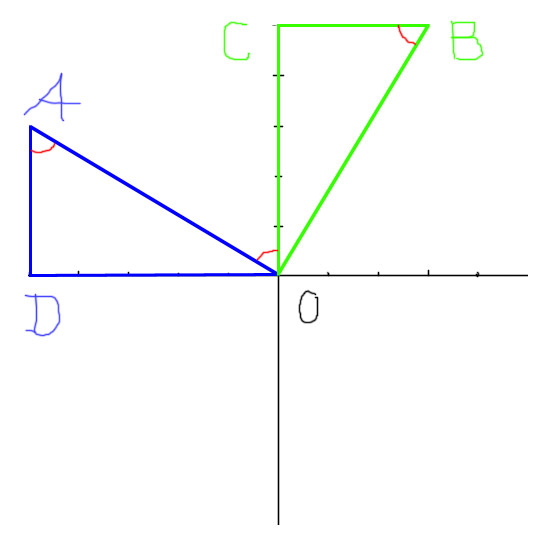