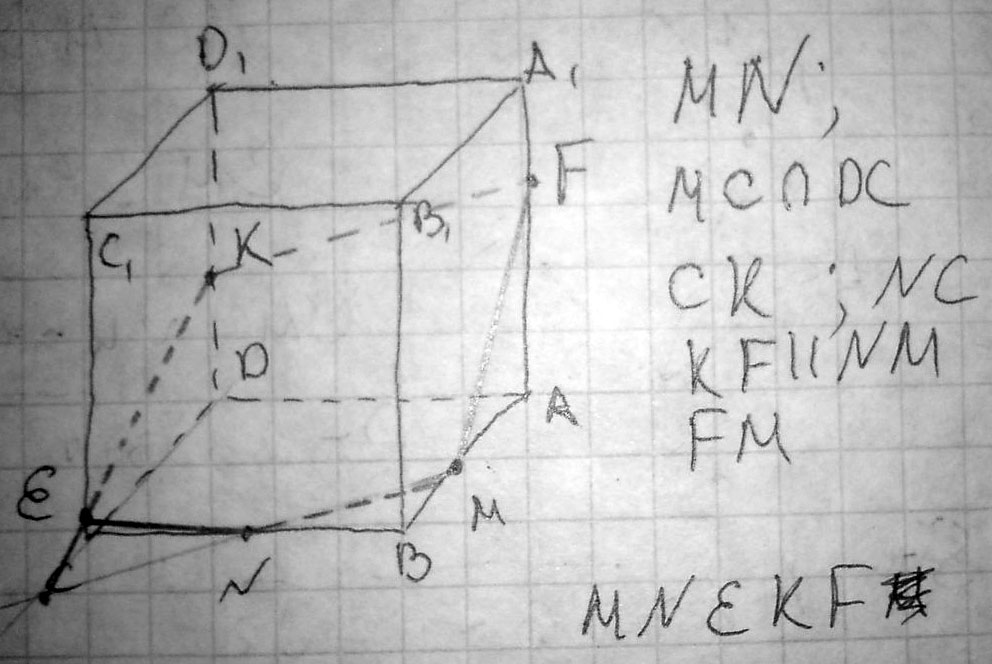
Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящей через точки М, N, К, являющиеся серединами ребер АВ, ВС, DD1.
Каждое ребро тетраэдра DABC равно 2см. Постройте сечение тетраэдра плоскостью, проходящей через точки В, С и середину М ребра AD. Вычислите периметр и площадь сечения.

Решение:
Точки М и N лежат в одной плоскости, поэтому проводим прямую MN так, чтобы она выходила за пределы нижней грани в обе стороны (MN-одна сторона сечения). Проводим прямую DC так, чтобы она пересеклась с MN в точке Т. Проводим прямую ТК, она пересечет кант СС1 в точке Н. НК-вторая сторона сечения, NH-третья сторона сечения. Проводим прямую DA так, чтобы она пересеклась с NM в точке Р. Проводим прямую РК, она пересечет ребро АА1 в точке Е. ЕК-четвертая сторона сечения, ЕМ-пятая сторона сечения. МЕКНN-искомое сечение (пятиугольник).
С тетраэдром проще. Соединяем точки С, М и В, это и есть сечение (равнобедренный треуг. СМВ). Грани тетраэдра - правильные треуг. и так как М-середина AD (АМ=MD=1см), то она медиана и высота. МС=МВ=√(4-1)=√3см Р=√3+√3+2=2+2√3см. Площадь можно было бы по формуле Герона, но периметр вышел некрасивый, поэтому проведем в треуг СМВ высоту МН. МН=√(МС^2-CH^2)=√(3-1)=√2см. S=1/2*2*√2=√2cм^2