АВСД-квадрат. Отрезок ПД перпендикулярен плоскости АВС. Доказать, что ПВ перпендикулярен АС.

Решение:
AC является диагональю квадрата ПВ и ДВ составляют ВД - вторую диагональ квадрата По свойству квадрата: диагонали в нём взаимно перпендикулярны! Следует что ВД перпендикулярно АС; следует ПВ перпендикулярно АС

PD-перпендикуляр, проведённый из точки P к плоскости (ABC); D-основание перпендикуляра; PB-наклонная; B-основание наклонной. Значит DB-проекция наклонной на плоскость. Но DB перпендикулярна AC(т.к. в квадрате диагонали перпендикулярны) Проведём прямую а параллельную AC через основание наклонной(через В). По лемме о перпендикулярности прямых(если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой): DB перпендикулярна a По теореме о трёх перпендикулярах(прямая(a), проведенная в плоскости через основание наклонной(B) перпендикулярно к ее проекции(DB) на эту плоскость, перпендикулярна и к самой наклонной(PB)):PB перпендикулярна a. И опять по лемме о перпендикулярности прямых:a||AC, a перпендикулярна PB, значит AC перпендикулярна PB.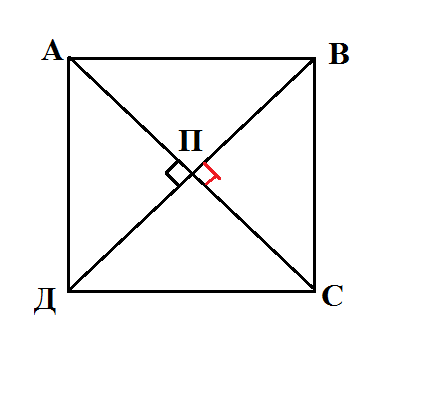