От равностороннего треугольника, площадь которого равна 36 см, отрезали три равных равносторонних треугольника так, что образовался правильный шестиугольник. Найдите площадь этого шестиугольника

Решение:

Сделаем построение по условию

обозначим стороны МАЛЫХ равносторонних треугольников  - х

тогда   у БОЛЬШОГО  - 3х

в равносторонних треугольниках все углы  60 град

площадь БОЛЬШОГО  Sb = 1/2 *3x*3x*sin60 =1/2 *9x^2*sin60

площадь МАЛОГО        Sm = 1/2 *x*x*sin60     =1/2 *x^2*sin60

по условию площадь БОЛЬШОГО  Sb = 36 см2

найдем площадь МАЛОГО 

Sm/Sb = 1/2 *x^2*sin60  /  1/2 *9x^2*sin60 = 1/9

Sm = 1/9 *Sb =1/9 *36 = 4 см2

по условию отрезали три равных равносторонних треугольника так что образовался правильный шестиугольник.

площадь шестиугольника

Sш = Sb - 3*Sm = 36 - 3*4 =36 -12 = 24 см2

ответ 24 см2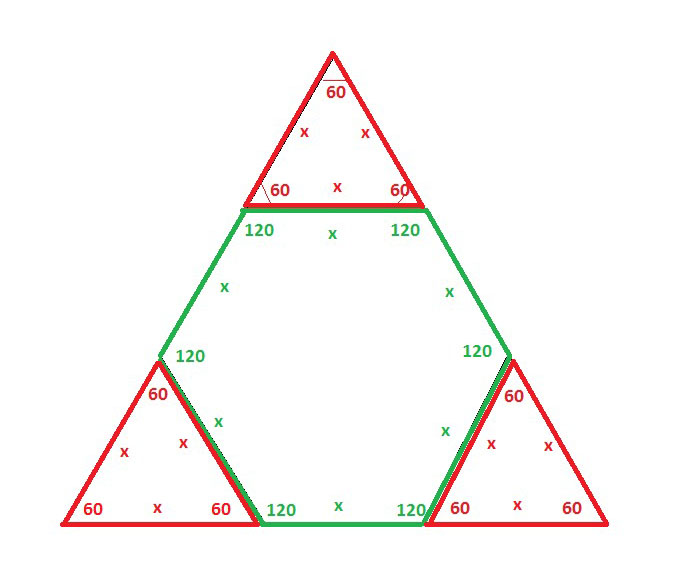

---

Отрезать от равностороннего треугольника равные между собой равносторонние треугольники так, чтобы остался шестиугольник, можно единственным образом: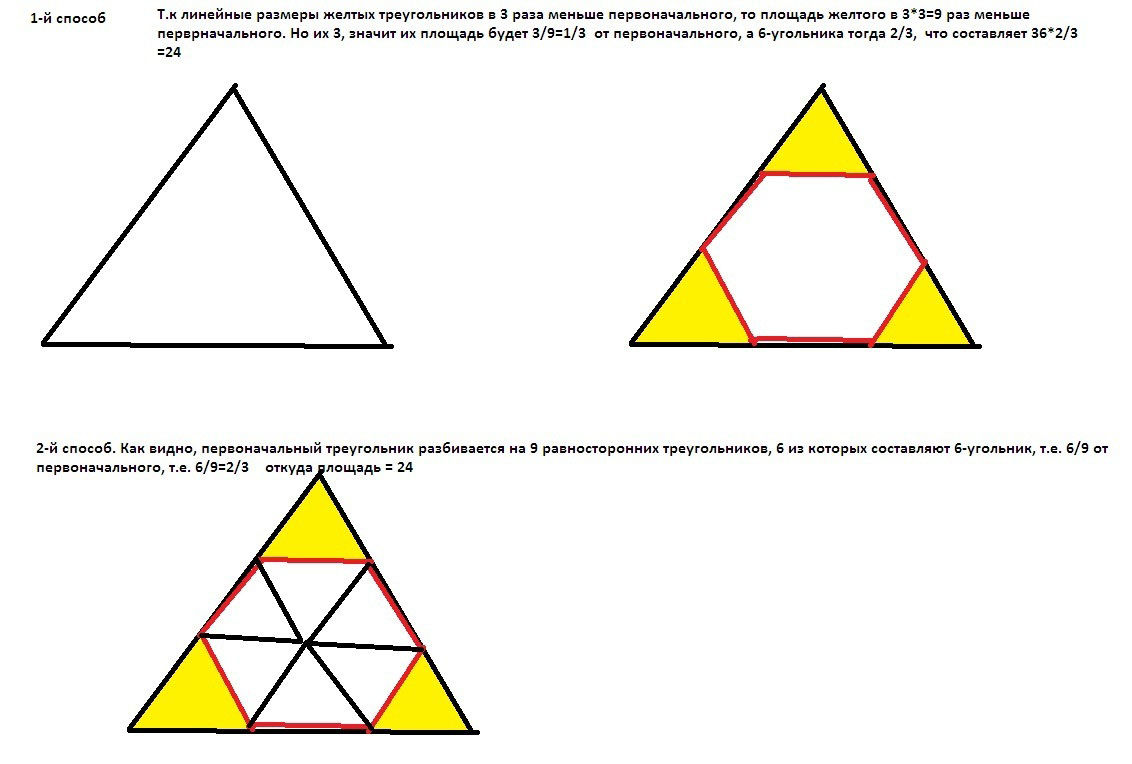
стороны данных треугольников равны сторонам шестиугольника, причём все стороны треугольников равны 1/3 стороне исходного треугольника.
Все треугольники будут подобны большему, коэффициент подобия равен 1/3.
Тогда их площади относятся как квадрат коэффициента подобия, т.е. 1/9.
Теперь найдём сумму площадей отрезанных треугольников:
Sотрез. = 3•1/9•36 = 36/3 = 12.
Площадь шестиугольника равна разности площади исходного треугольника и сумме площадей отрезанных треугольников:
Sшест. = 36 - 12 = 24.
Ответ: 24.