Острый угол ромба 60 градусов, а его площадь 54корнеь3. Найти длину большей диагонали ромба

Решение:
1. Площадь ромба $$ S=54\sqrt3 $$ за формулой $$ S=a^2sin\alpha, $$ где $$ \alpha $$ - острый угол между сторонами ромба, найдем его сторону: 54$$ 54\sqrt3=a^2sin60\\ $$
$$ a^2=\frac{54\sqrt3}{sin60}\\ $$
$$ a^2=\frac{54\sqrt3}{\frac{\sqrt3}{2}}={54\sqrt3}\cdot\frac{2}{\sqrt3}=54*2=108 $$
$$ a=\sqrt{108}=4\sqrt7 $$ 2.Диагонали ромба пересекаются под прямым углом, значит угол АОВ = 90 градусов. диагонали ромба также являются его бисектрисами. т.о. угол АВО=30. значит треугольник АОВ - прямоугольный (угол АОВ=90) с острым углом АВО = 30. и что следует с п.1 стороной $$а= 4\sqrt7 $$. 3. $$ cosABO=\frac{BO}{AB} \\ BO=AB\cdot cos{ABO} \\ BO=4\sqrt7 \cdot cos30 = 4\sqrt7 \cdot \frac{\sqrt3}{2}=2 \cdot \sqrt{21} $$
$$ BD=2*BO \\ BD=2*BD=2\cdot BO= 2 \cdot 2 \sqrt{21} = 4 \sqrt{21}$$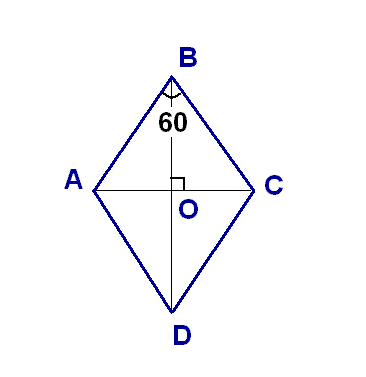