В прямоугольном треугольнике с острым углом 45 градусов гипотенуза равна 3 корень из 2 см. Найдите катеты и площадь этого треугольника.

Решение:
Решение:

1)АВ=3корень из 2=корень из 2*9=корень из 18

2)по теореме Пифагора

АС в квадрате+ СВ в квадрате=АВ в квадрате

АС в квадрате+ СВ в квадрате= 18

т.к. один из углов =45 градусов, то и второй тоже=45 градусов

из этого следует, что  треугольник равнобедренный (АС=СВ)

АС в квадрате=СВ в квадрате=18:2=9

корень из девяти=(+-)3

-3 не подходит по условию, сторона не может быть отрицательной

3) площадь треугольника=3см*3см:2=4,5 см в квадрате

---

Раз один угол 45 градусов, то идругой тоже 45, так как в треугольнике всего 180.А прямой у нас уже есть. а раз так, то треугольник равнобедренный и боковые стороны его равны.Пусть одна сторона равна А см.  И другая тоже А см.Тогда по теореме Пифагора (3√2)² = А²+А²

                                    9·2=2А²

                                     2А²=18

                                      А²=9

                                        А= √9=3 см

Оба катета по 3 см.

Площадь прямоугол. треугольника равна половине произведения их катетов.Значит, (3·3)/ 2 = 4,5 см²

ОТВЕТ:площадь 4,5 см², оба катета по 3 см 

Так как треугольник прямоугольный, да еще и с углов в 45 градусов, то отсюда следует что оба катета равны, а по теореме Пифагора: квадрат гипотенузы равен сумме квадратов двух катетов, т.е. 3кв.корня из 2 возводим в квадрат...

(3кр.2)^2=9*2=18(без кв. корня)

18/2=кв.корень из9

кв.корень из 9=3

Ответ: оба катета равны 3см.

---

Данный прямоугольный треугольник - равнобедренный, поэтому:

c²=2a²

а²=с²/2= (3√2)²/2=18/2=9

а=3 (см)

S=0.5а²=0,5*9=4,5 (см²)

один из углов 45, значит второй тоже 45, а значит этот треугольник равнобедренный(т.к. углы при основании равны.)

Значит боковые стороны у него равны, а то есть катеты.

катет можно обозначить за x.

значит второй тоже x.

По теореме Пифагора(квадрат гипотенузы равен сумме квадратов катетов) составляем уравнение

$$ x^{2}+x^{2}=(3\sqrt{2})^{2} $$

$$ 2x^{2}=18 / $$ делим на 2

$$ x^{2}=9 $$

x=3  x=-3(не удов. усл. зад.)

катеты будут равны 3 см.

S треугольника= половина основания на высоту, т. е. 1/2 катет на катет, в нашем случае

S=1/2*3*3=4,5 см(в квадр.)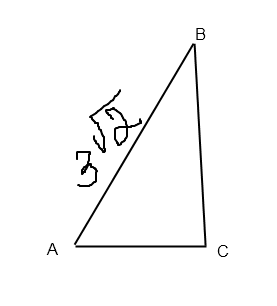