№1. \(\Delta\)АВС ~ \(\Delta\)КДМ. Отношение их периметров равно 3:4. Найти отношение площадей этих треугольников и коэффициент подобия.
№2. На рисунке АВ||СД. А) Докажите, что АО : ОС = ВО : ОД.
6) Найдите АВ, если ОД=15см, ОВ=9см, СД=25 см.

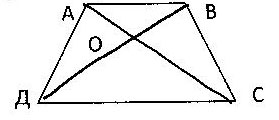Решение:
№1. Обобщённая теорема подобия гласит, что если два треугольника подобны, то любой линейный элемент одного треугольника относится к соответствующему линейному элементу другого треугольника как соответственные стороны. Периметр - сумма длин сторон, линейный элемент. Если периметр одного треугольника относится к периметру другого как 3/4, а сами треугольники подобны, то 3/4 - это и есть коэффициент подобия. k=3/4 Отношение площадей подобных фигур равно квадрату коэффициента подобия: S KDM/S ABC=(3/4)^2=9/16 Ответ: отношение площадей 9/16, k=3/4.
№2. ABCD - трапеция (по определению: АВ || CD, ВС не параллельна AD) а) Диагонали трапеции разбивают её на 4 треугольника, причём треугольники, прилежащие к основаниям подобны друг другу (по свойству трапеции). Рассмотрим треугольники АВО и CDO: они подобны. Следовательно, АО:ОС=ВО:OD. б) Так как треугольники АВО и CDO подобны, то АВ:СD=ВО:OD АВ:25=9:16 АВ=0,5625*25=14,0625 (см) Ответ: АВ=14,0625 см.