1. В шаре на расстоянии 12 см от центра проведено сечение площадью 64π. Найти площадь поверхности сферы.
2. Площадь сечения, удаленного от центра шара на 21 см, равна 784π Найти площадь поверхности сферы.

Решение:

Обе задачи решаются однотипно.
Площадь сферы находят по формуле
S=4πR²
Для наглядности сделаем схематический рисунок осевого сечения шара, перпендикулярного данному сечению.
Сечение шара - круг. На рисунке он в разрезе выглядит линией.
АВ - его диаметр, а МВ- радиус.
ОМ - расстояние от центра круга до центра плоскости сечения, ОВ- радиус шара.

1) Найдем квадрат радиуса сечения из его площади.
S=πr²
64π=πr²
r²=64
Из прямоугольного треугольника ОМВ по т. Пифагора найдем R² шара.
R²=64+144=208
S=4πR²=4*208π=832π
2) Найдем квадрат радиуса сечения из его площади.
784π=πr²
r²=784
R²=784+21²=441
S=4πR²=4π*441=1764π
-
Если есть необходимость, можно вычислить площадь, умножив на π- в этом поможет калькулятор.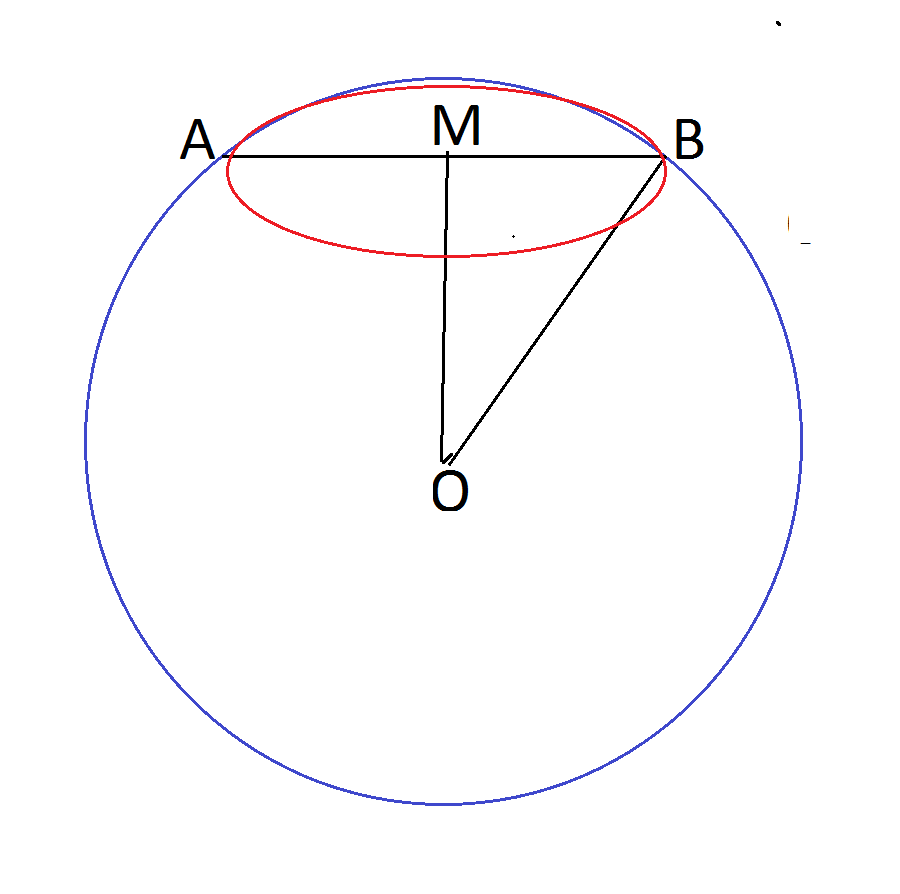