Вычислите объем и площадь поверхности шара, если площадь сечения, проходящего через центр шара равна 64π см в квадрате. Ответ укажите c точностью до целых

Решение:

Сечение проходящее через центр шара, является осевым сечением, и представляет из себя круг. Тогда площадь сечения будет равна:

\( S=\pi R^2 \)

Отуда находим радиус сечения

\( R=\sqrt{\frac{S}{\pi}}=\sqrt{\frac{64\pi}{\pi}}=8 \)

Так как сечение является осевым, радиус шара будет равен радиусу сечения, тогда площадь шара будет равна:

\( S=4\pi R^2=4\pi 8^2=256\pi\approx803 cm^2 \)

А объем шара будет равен:

\( V=\frac43 \pi R^3=\frac 43 \pi 8^3=\frac{2048}{3}\pi\approx2143 cm^3 \)

Ответ: \( S\approx803 cm^2 \)

               \( V\approx2143 cm^3 \)

Сечение, перпендикулярное диаметру шара, делит этот радиус пополам. Площадь поверхности шара равна 144 π. Найдите объем большего шарового сегмента, отсекаемого от шара.

Объем шарового сегмента находят по формуле 

                          V=π•h²•(3R-h):3

Из площади поверхности шара найдем R 

4πR²=114. ⇒R²=36 ⇒ R=6 

Высота сегмента равна R+0,5R=6+3=9

V=π•81•(18-9):3=243π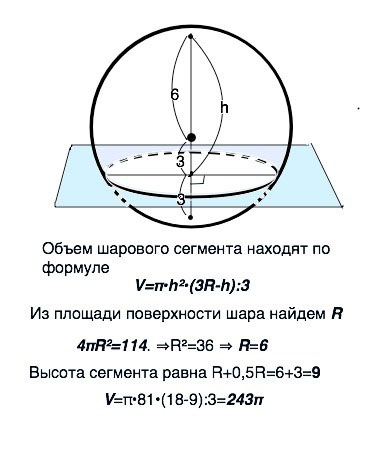

Вершины равностороннего треугольника со стороной 5корня из 3 см лежат на поверхности шара а растояние от центра шара до площади треугольника равно 12. Найти площадь поверхности шара

Назовем треугольник АВС. Центр описанной около треугольника окружности О лежит на пересечении серединных перпендикуляров АА1, ВВ1 и СС1. Рассмотрим треугольник АОВ1:  угол ОАВ1=60/2=30. Тогда ОВ1 – катет, лежащий против угла в 30 градусов, значит АО=2ОВ1. Примем ОВ1 за х. АВ1=АС/2=5 корня из 3/2. Тогда:

АО^2-OB1^2=AB1^2

(2х)^2-х^2=(5 корня из 3/2)^2. Отсюда х=2,5=ОВ1; АО=2*2,5=5=r

Пусть О1 – центр шара. Рассмотрим треугольник ОАО1:

О1А^2=AO^2+OO1^2=5^2+12^2=25+144=169; О1А=13

S=4*пи*R^2=4*пи*О1А^2=4*3,14*13^2=2122,64

Сечение, перпендикулярное диаметру шара, делит этот диаметр в отношении 1 : 3. Найдите объем меньшего шарового сегмента, отсекаемого от шара, если площадь поверхности шара равна 144 π.

Сечение, перпендикулярное диаметру шара, делит этот диаметр в отношении 1:3.

Значит, высота отсекаемого сегмента равна D/4=R/2

Из формулы площади поверхности сферы

R=√(144:π)=6/√π

Высота h сегмента равна R/2=3/√π

Формула объёма  шарового сегмента 

V=π•h²•(3R-h):3

V=π•9•(18-3):3√π =45/√π = ≈ 25,39 (ед. объёма).