Из точки М проведён перпендик. MD=4см. К плоскости прямоуг. ABCD наклонные МА и МС образуют плоскости треуг. Угол45и 30 соответст. Найти стороны прямоуг.

Решение:
Треуг.ADM - п/у т.к. MD - перп. плоскости); треуг. ADM - р/б (т.к. Угол МАС=45гр.) Следовательно DM=AD=4. угол MCD=30гр. следовательно MD=1/2MC MC=8 CD=$$ \sqrt{MC^{2}-MD^{2}}=4\sqrt{3} $$

Прямая MD перпендикулярна к плоскости, а значит она перп к любой прямой лежащей в этой плоскости(по определению перпен. прям и плоск.). Значит треугольники AMD и MDC-прямоугольные.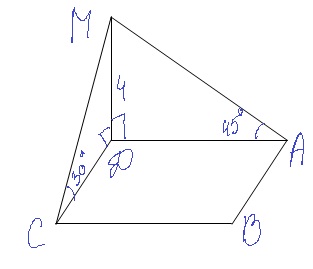
Рассмотрим треуг. MDC.MD=4, а угол MDC=30град.Катет, лежащий против угла в 30град=половине гипотенузы; следовательно MC=8.И по Пифагору находим сторону DC прямоугольника.Она = 4√3.
Далее рассмотрим треуг. AMD.Угол MAD=45град., значит треугольник равнобедреный,и сторона AD прямоугольника тоже = 4.
Ответ:стороны прямоугольника равны 4 и 4√3.