В параллелограмме ABCD диагонали пересекаются в точке O, K - середина стороны AB, AK = 3 см, KO = 4 см. Найдите периметр параллелограмма. Сравните углы KOA и BCA.

Решение:
Подробное решение. 
Параллелограмм - четырехугольник с попарно параллельными и равными сторонами. 
По условию АК=АВ=3 см.  ⇒АВ=АК+КВ=3+3=6 см
СD=АВ=6 см 
Диагонали параллелограмма точкой пересечения делятся пополам. 
⇒  ВО=ОD, а КО - средняя линия треугольника АВD, т.к. делит его боковые стороны пополам. 
КО, как средняя линия треугольника, параллельна его основанию АD,
Т.к. диагональ параллелограмма делит его на два равных треугольника,  средние линии в треугольниках АВС и ВСD равны. 
КО=ОМ ⇒ 
КМ=4+4=8 см 
КМ - параллельна и равна АD=ВС
АD=ВС=8 см
1) Периметр АВСD=АВ+СD+ВС+АD=2*6+2*8=28 см 
2) Сравните углы KOA и BCA.
Углы КОА и ОАД накрестлежащие при  пересечении двух параллельных прямых третьей ( секущей СА). Такие углы равны. 
Угол ВСА=углу САD на том же основании: это накрестлежащие углы, образованные пересечением параллельных прямых секущей АС. 
⇒ Так как угол КОА=углу ОАD, а угол ОАD=углу ВСА, - угол КОА=углу ВСА. 
С другой стороны, можно рассмотреть эти углы как соответственные при пересечении параллельных ВС и КМ секущей АС.
Соответственные углы при этом равны; равенство углов КОА и ВСА доказано дважды.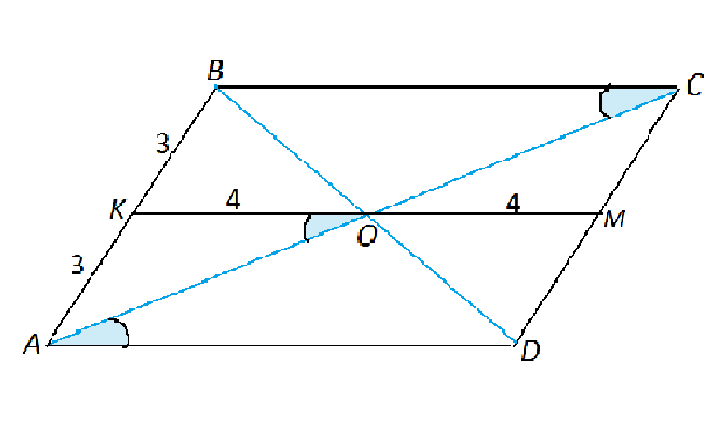