В треугольнике ABC, AC=CB=8, угол ACB= 120°. Точка M удалена от плоскости треугольника на расстоянии 12 см. Точка M удалена от плоскости треугольника на расстоянии 12 см и находится на равном расстоянии от вершин треугольника ABC. Найти угол между MA и плоскостью треугольника ABC

Решение:
В треугольнике ABC, AC=CB=8, угол ACB= 120°.  Точка M удалена от плоскости треугольника на расстоянии 12 см и находится на равном расстоянии от вершин треугольника ABC. 

Найти угол между MA и плоскостью треугольника ABC Точка M  находится на равном расстоянии от вершин треугольника ABC, следовательно, наклонные МА, МС и МВ равны, их проекции также равны, а  М проецируется в центр О описанной вокруг ∆ АВС окружности.  ОА=ОВ=ОС=R Углы при А и В равны, как углы при основании равнобедренного треугольника. ∠А=∠В=(180º-120º):2=30º По т.синусов R=(AC:sin 30º):2=(8:0,5):2=8 см ∆ МOA - прямоугольный, МО=12, ОВ=8, и tg ∠MAO=12/8=1,5 ∠MAO = ≈56º20’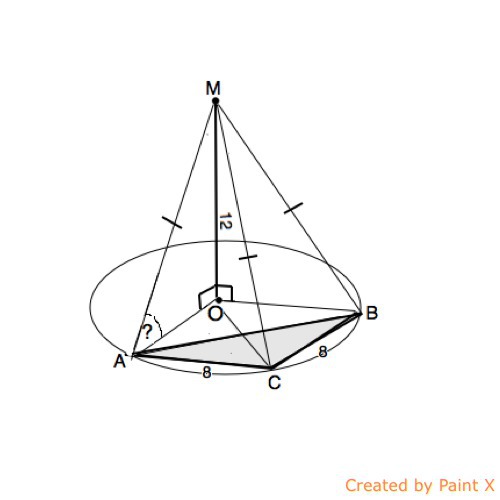