К плоскости ромба ABCD, у которого угол А равен 45°, АВ=8см, проведен перпендикуляр МС длиной 7см. Найдите расстояние(длину перпендикуляра) от точки М до прямой АВ

Решение:
Продолжим сторону АВ от точки В на некоторое расстояние. Из точки С опустим перпендикуляр на это продолжение до пересечения в точке К. Затем соединим точку М с точкой К. МК и есть искомое расстояние. Сначала найдём КС=ВС умноженное на cos45=8 на 0,71=5,68. Угол КСВ=45 поскольку треугольникКСВ прямоугольный а угол КВС также равен 45 потому что СВА=135. По теороме Пифагора КМ=корень из суммы квадратов( КС квадрат + МС квадрат)=9.

построй рисунок ---начни с угла А=45---углы В С D точка М висит над углом С---найти расстояние от М до АВ сделай дополнительное построение---над вершиной D построй точку М1 (это параллельный перенос)---тогда М1D=MC=7см---из вершины D опусти перпендикуляр на АВ в точку К (это расстояние от D до АВ)--тогда DK это проекция М1К на  плоскость ромба--это и есть расстояние от т. М(М1) до прямой АВ теперь длина М1К= треуг.АКD прямоугольн.--угол К =90--угол А=45---- сторона АD=8см, т.к. все стороны ромба равны--тогда КD=AD*sin45=8*√2/2=4√2 см треуг.КDM1 прямоугольн---угол КDM1=90(это перпендикуляр к плоскости) КМ1-гипотенуза КМ1=√(М1D)^2+(DK)^2=√( 7^2+(4√2)^2)=√49+32=√81=9см расстояние от точки М до прямой АВ ==9см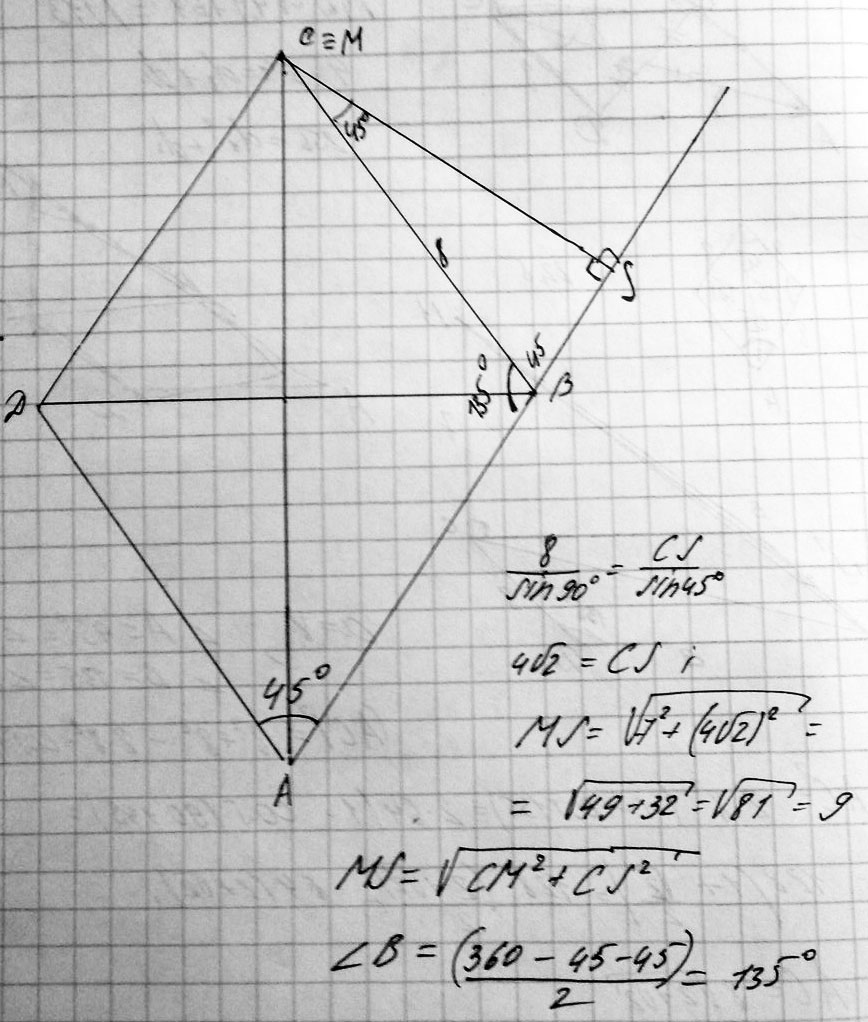