Сторона основания правильной треугольной пирамиды равна 4, а двугранный угол при основании равен 45°. Найдите объём пирамиды.

Решение:
В пирамиде SABC проведем высоту SO. Так как пирамида правильная, эта высота совпадает с центром треугольника в основания. В грани SAB проведем апофему SH. Треугольник SOH прямоугольный с углом SHO, равным 45°, значит, он равнобедренный, и OH=SO. OH=1/3CO, так как O - точка пересечения медиан, а CO - медиана. Тогда OH=2sqrt(3)/3, SO=2sqrt(3)/3. Площадь основания находим по формуле S=sqrt(3)a^2/4, здесь a=4, тогда S=4sqrt(3). V=1/3SH, отсюда V=1/3*2sqrt(3)/3*4sqrt(3)=2.

---

Так как двугранный угол 45°, то треугольник, образованный высотой пирамиды и высотой боковой грани - равнобедренный, а значит высота пирамиды равна 13 медианы основания.
Медиана основания равна сторона основания умножить на √3 разделить на 2.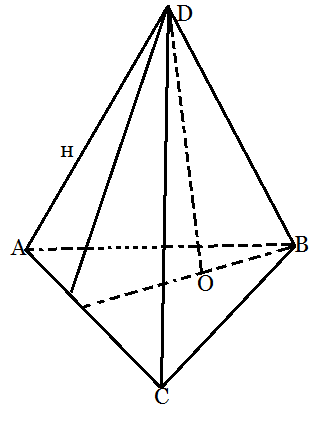