Около квадрата со стороной 2^2 описана окружность которая вписана в правильный треугольник. Найдите площадь треугольника.

Решение:
Дано:а=2 сторона квадрата, АВС правильный треугольник. Найти: Sавс. Решение: Д - диагональ квадрата. По теореме Пифагора Д^2 = а^2 + а^2 Д=кор.кв.( 2 х  а^2) = а х кор.кв.2=   2 х кор.кв.2  Д является диаметром описанной окружности около квадрата. Следовательно радиус окружности  r=1/2 х Д =  кор.кв.2 Радиус окружности вписанной в правильный многоугольник находится по формуле:   r = А  / (2 х tg(180/n)) , где  А сторона многоугольника ,  n угол   многоугольника.    r = А  / (2 х tg(180/60))  =   А /6 х  ( кор.кв.3 )  А =   (6 х r)  /   ( кор.кв.3) =   (6 х   ( кор.кв.2) )  /   ( кор.кв.3)   Sавс = А х H  /  2 ,  H высота правильного треугольника.   По теореме Пифагора  А ^2 = (А / 2) ^2  +  H^2   H ^2  =  А ^2 - (А / 2) ^2 = 3 х А ^2 / 4     H  =( кор. кв. 3 х А)  / 2    Sавс = А х H  /  2 =  Sавс =( А / 2)  х  ( кор. кв. 3 х А)  / 2 = ( кор. кв. 3 х А ^2 )  / 4 = (36 х 2 х  ( кор. кв. 3 )) /( 3 х 4) = 6 х ( кор. кв. 3 )     Ответ:  Sавс =   6 х ( кор. кв. 3 )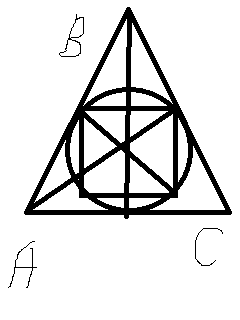