Средняя линия равнобедренной трапеции равна 8, угол при одном из оснований равен 135°, а боковая сторона равна 5. Найдите площадь трапеции

Решение:
Дано: КL=8 (средняя линия,на рисунке нет), ∠B=135 гр. AB=5 Найти: S трапеции Решение: 1. Площадь трапеции находится по формуле $$ S=L*h $$, где L- это средняя линия, h - высота трапеции. Т.е. нужно найти высоту. 2. Доп.построение: опускаем высоту $$ BB_{1} $$ 3. Т.к. ∠В=135, а трапеция равнобедренная, то ∠С= 135, а углы А и D: ∠A+∠D = 360 - 135*2=90, а так как они равны , то ∠A=90:2=45 4. Рассмотрим треугольник $$ ABB_{1} (B_{1} = 90)$$ найдем $$ BB_{1} $$ через sin∠A: $$ sinA=\frac{BB_{1}}{AB}=\frac{BB_{1}}{5} \\ sin 45= \frac{\sqrt{2}}{2} $$, подставляем $$ \frac{\sqrt{2}}{2} = \frac{BB_{1}}{5}$$, выражаем отсюда $$ BB_{1} = \frac{\sqrt{2}*5}{2}$$, это и есть искомая высота 5. Подставляем в формулу $$ S= 8*\frac{\sqrt{2}*5}{2} = 20\sqrt{2}$$ Ответ: $$ S=20\sqrt{2}$$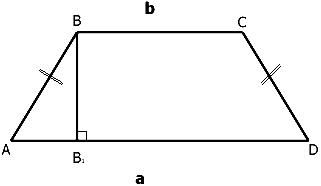