Внутри параллелограмма АВСD отмечена точка М. Докажите, что сумма площадей треугольников AMD и BMC равна половине площади параллелограмма.

Решение:
проведем через точку М, пряммую перпендикулярную АD, так как AD||BC, то она будет перпендикулярна и прямой ВС, пусть прямую AD она пересекает в точке L, а прямую BC в точке K. Тогда LM - высота параллелограмма ABCD, LM - высота треугольника ADM, KM - высота треугольника BCM.
Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне Площадь треугольника равна половине произведения стороны на высоту проведенной к этой стороне
Поэтому S(AMD)+S(BMC)=1/2*AD*LM+1/2*BC*KM=так противоположные стороны параллелограмма равны= =1/2*AD*LM+1/2*AD*KM=1/2*AD*(LM+KM)=1/2*AD*LK=1/2*S(ABCD), что и требовалось доказать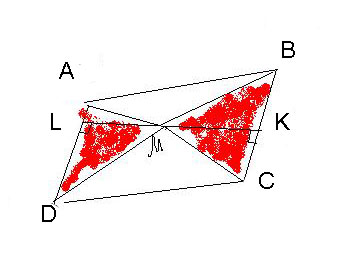