Докажите, что диагональ четырёхугольника меньше его полупериметра.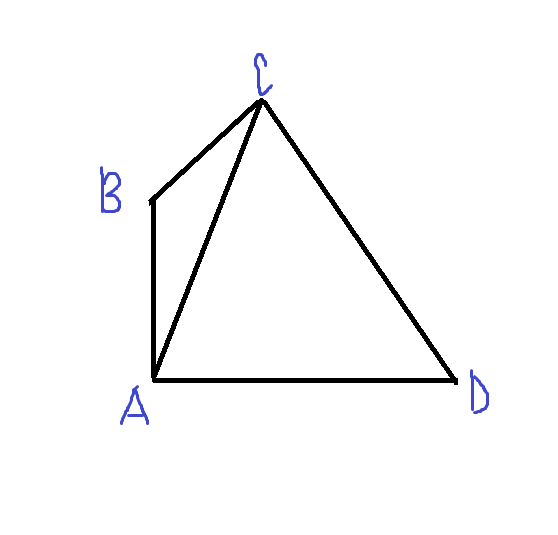

Решение:
Обозначим стороны четырехуг. и диагональ:
a,b,c,d и e.
Тогда каждая диагональ будет общей стороной двух треугольников.
Тогда используя неравенство треугольника можно записать:
a+b>е
c+d>e
Складываем эти неравенства:
a+b+c+d > 2e.
То же можно написать для другой диагонали.

Напишем очевидные неравнества (называются неравенством треугольника): AC <= AB + BC, AC <= AD + CD.
Сложим эти неравенства: 2AC <=   AB + BC +  AD + CD. Поделив обе части на 2, получим AC <=  ( AB + BC +  AD + CD)/2. Слева диагональ, справа полупериметр, что и требовалось доказать.  Точнго так же доказывается и для диагонали  BD ))