В шар по одну сторону от центра проведены два параллельных сечения площади которых равны 40π см² и 4π см². Найдите площадь сферы, если расстояния между сечениями равно 9см.

Решение:

Площадь сферы S = 4*pi*R² 
где R - радиус шара
параллельные сечения представляют из себя окружности с радиусами 
r1 = √40 
r2 = √4 
из получившихся прямоугольных треугольников можно записать:
R² = (r1)² + x²
R² = (r2)² + (x+9)²
-
40 + x² = 4 + x² + 18x + 81
18x = 40-85 = -45
-где-то ошибка в данных) 
если расстояние от центра шара до бО’льшего сечения обозначить (х) - оно 
ведь будет ближе к центру, а расстояние от центра шара до меньшего сечения обозначить (у) - оно будет дальше от центра
у > x
можно записать (r1)² + x² = R² = (r2)² + y²
(r1)² - (r2)² = y² - x²
40 - 4 = 36 = (y - x)(y + x)
и по условию расстояние между сечениями 9 = у - х
а т.к. Произведение = 36, то на сумму (х+у) остается 4
сумма двух (положительных !) чисел МЕНЬШЕ их разности)
противоречие)
а с точки зрения чертежа - с таким расстоянием между сечениями около них окружность не опишется.
эллипс получится)
или сечения по разные стороны от центра)
ход решения, думаю, уже очевиден.
найти х - вычислить R - подставить его в формулу для S)))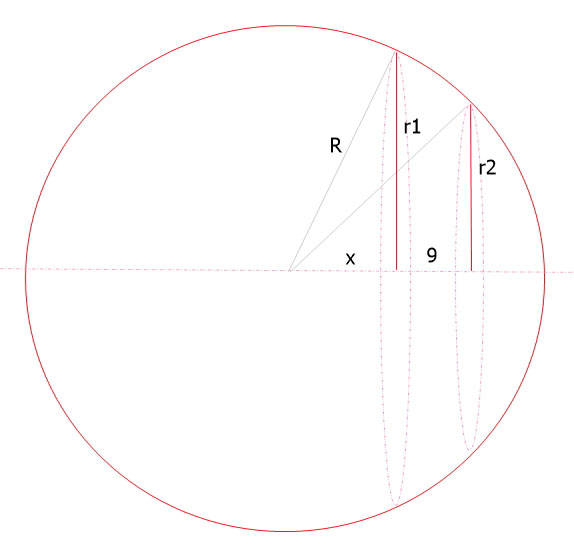