Докажите, что отрезки касательных, проведенных к окружности из одной точки, равны.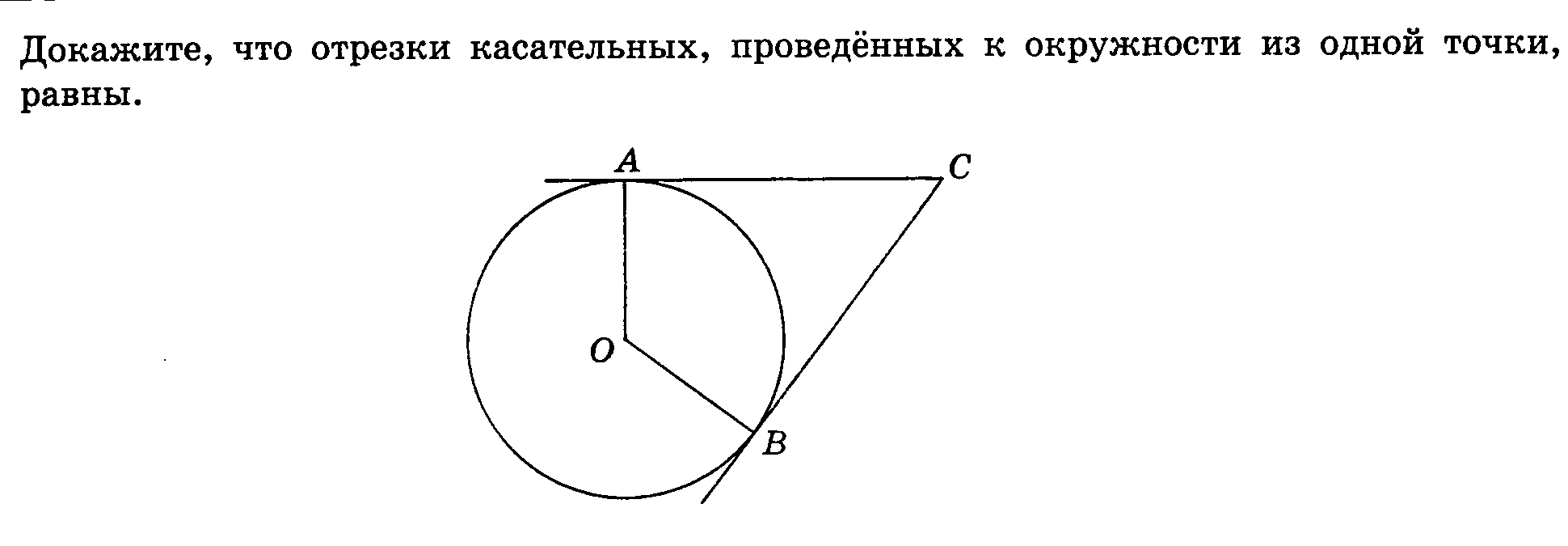

Решение:
Проведем СО и рассмотрим  треугольники ОAC и OBC 1) В ΔОAC и ΔOBC: ОC — общая, ОA = OB, как радиусы, ОA ⊥ CA, OB ⊥ CB (т.к. AC и CB — касательные). Таким образом, ΔОAC = ΔOBC по 1-му признаку равенства треугольников. Откуда AC = CО. 2) Пусть через точку C можно провести три касательных к окружности: CA, CB, CM. Тогда следует, что CA = CB = CM, откуда точки A, B, M лежат на одной окружности с центром C. Получилось, что две окружности имеют три общие очки. Противоречие. Теореме  об окружности:окружности не могут пересекаться  более чем в двух точках. Таким образом, через данную точку нельзя провести более двух касательных к данной окружности.Поэтому  СA и СВ касательные к окружности и они равны .

Из точки С проведем отрезок СО. Получим два треугольника:ΔСОА и ΔСОВ В ΔСОА и ΔСОВ: СО — общая, ОА = OВ, как радиусы, ОА ⊥ СА, OВ ⊥ СВ (т.к. СА и СВ — касательные). Таким образом, ΔСОА = ΔСОВ по 1-му признаку равенства треугольников. Откуда СА = СВ.