В треугольник АBC известны стороны АС=2, AB=3. BC=4. На прямой АС взята точка D отличная от С так что треугольник ABD подобен треугольнику АСВ. Найдите BD а также расстояние от D до середины BC

Решение:
Точка D выбирается так, что угол BDA = угол CBA; Обозначим его за Ф. тогда в треугольниках АВС и ABD все углы попарно равны; Сторона АВ в ABD соответствует стороне АС в АВС - это видно из соответствия углов и сторон;  Поэтому ABD имеет все линейные размеры в 3/2 раза больше (его стороны равны 3; 4,5; 6). То есть BD = 6. Отсюда, кроме того, DC = 2,5.  Надо вычислить длину медианы DM в треугольнике BDC. См чертеж. Из достроенного тр-ка CDD1 (СD1 II BD) по теореме косинусов (2*m)^2 = x^2 + z^2 + 2*x*z*cosФ; А из тр-ка BDC  y^2 = x^2 + z^2 - 2*x*z*cosФ; здесь y = ВС. Складываем, и получаем выражение для квадрата медианы через квадраты сторон )) m^2 = (2*x^2 + 2*z^2 - y^2)/4; Подставляем x = 6, y = 4, z = 2,5. получаем  m = корень(30)*3/4
Чертеж, поясняющий, как строится треугольник BDA: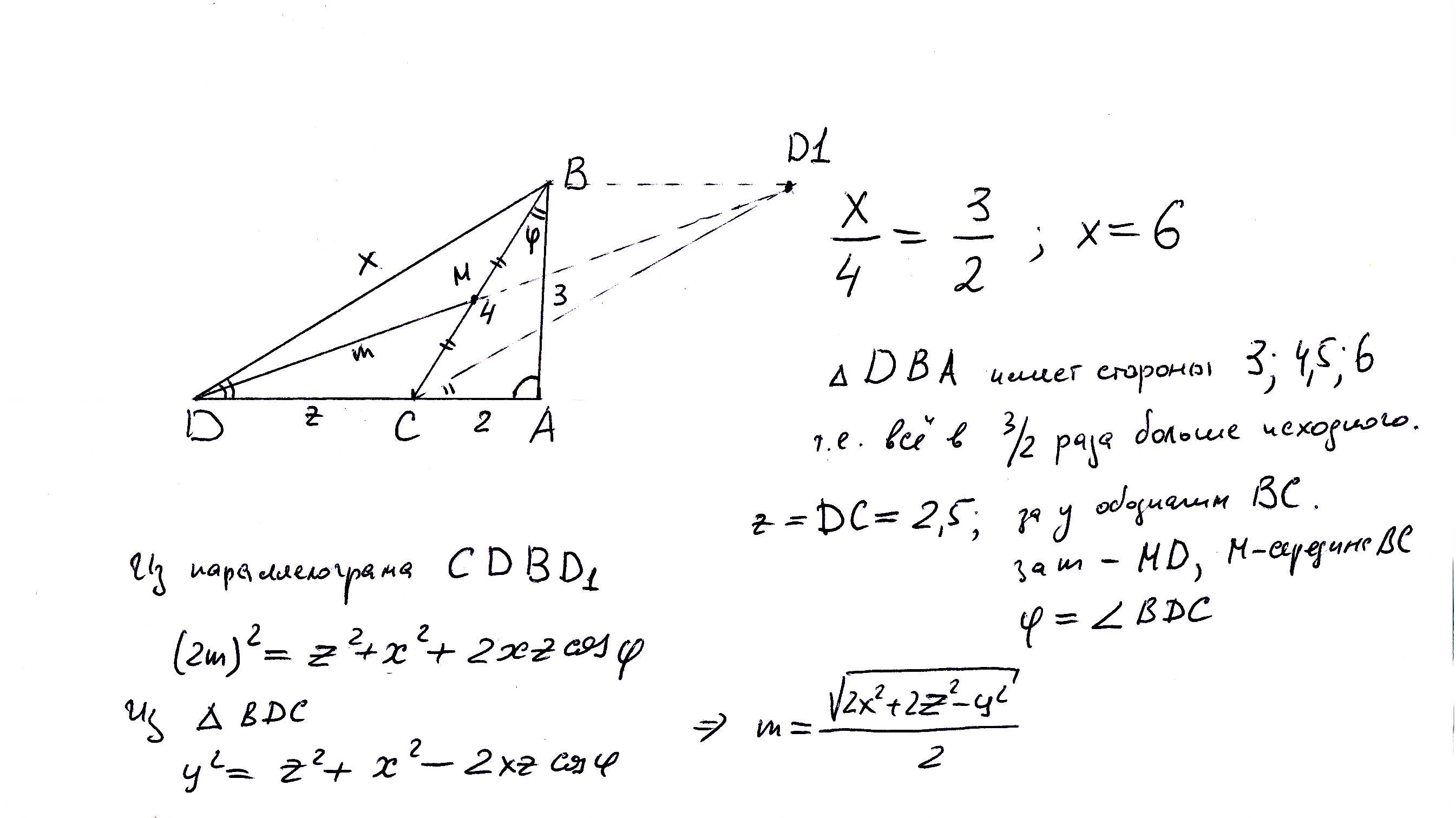