Найти площадь Δ АВС по чертежу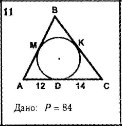

Решение:
периметр P = 84, полупериметр p = 42; одна сторона а = 26,  поскольку МВ = ВК (обозначим их за х), b = 12 + x; c = 14 + x; 2*x = p - 2*26; x = 16; b = 28; c = 30; стороны нашли. ну, далее - формула Герона S = корень(p*(p-a)*(p-b)*(p-c)) =  корень(42*16*14*12) = 336;
Кстати, формулу Герона не так-то просто доказать. Если заданы стороны треугольника, то площадь выражается через произведение сторон и угол между ними 2*S = a*b*sinC; Есть еще теорема косинусов с^2 = a^2+b^2 - 2*a*b*cosC; Отсюда выражаются синус и косинус через площадь и стороны, потом возводятся в квадрат (!) и складываются (ну, (sinC)^2 + (cosC)^2 = 1; как известно )) После некоторых манипуляций с выражением получается формула Герона.
Доказательство ниже