Из концов диаметра АВ окружности опущены перпендикуляры АА1 и ВВ1 на касательную. Докажите, что точка касания С является серединой отрезка А1B,.

Решение:
Рассмотрим окружность, которая у нас получилась, зная, что радиус перпендикулярен к касательной, проведенной в точку касания,то прямые  A1B1 И AB  параллельны  угол1 =углу2 КАК (ПЕРПЕНДИКУЛЯРЫ) следовательно прямые параллельны значит расстояния межу ними равные т.е а1в1 и ав рассмотрим два квадрата, равны значит в1с=са1 те с=12 A1B1

Пусть О -центр окружности Прямые АA1, BB1 и ОС параллельны, так они перпендикулярны одной и той же прямой А1В1.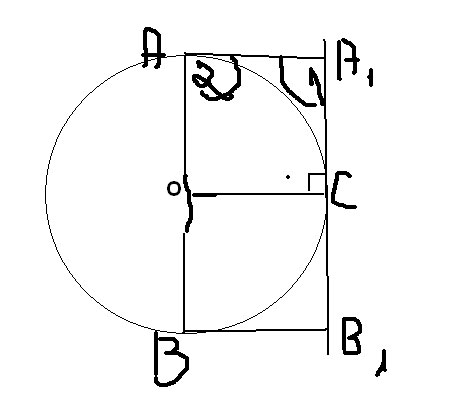
Так как прямая ОС делит пополам отрезок АВ, то она делит пополам и отрезок А1В1 по теореме Фалеса, т.е. точка С является серединой отрезка А1В1, что и требовалось доказать. Доказано