Через вершину прямого угла C равнобедренного прямоугольного треугольника ABC проведена плоскость альфа, параллельная гипотенузе и составляющая с катетом угол 30°. Найдите угол между плоскостью ABC и альфа. Решить, желательно подробно и с рисунком.

Решение:
См. чертеж. М - середина АВ. Плоскость альфа - это плоскость СВ1А1. Прямая В1А1 - проекция () прямой АВ на "альфа". Прямая, проходящая через С и параллельная АВ и А1В1 - это ребро двугранного угла между плоскостями АВС и "альфа". По условию, угол АСА1 = 30°. Это означает, что расстояние между прямой АВ и плоскостью "альфа" равно АС*sin(30) = AC/2; То есть ММ1 = АС/2. МС = АС/корень(2) поэтому sin(M1CM) = M1M/MC = (AC/2)/(АС/корень(2)) = корень(2)/2 Значит угол М1СМ = 45°м.
Ясно, что оба отрезка перпендикулярны ребру двугранного угла, так как в равнобедренных треугольниках (АВС и А1В1С) они являются медианами к основанию, а значит, высотами, основания же параллельны ребру.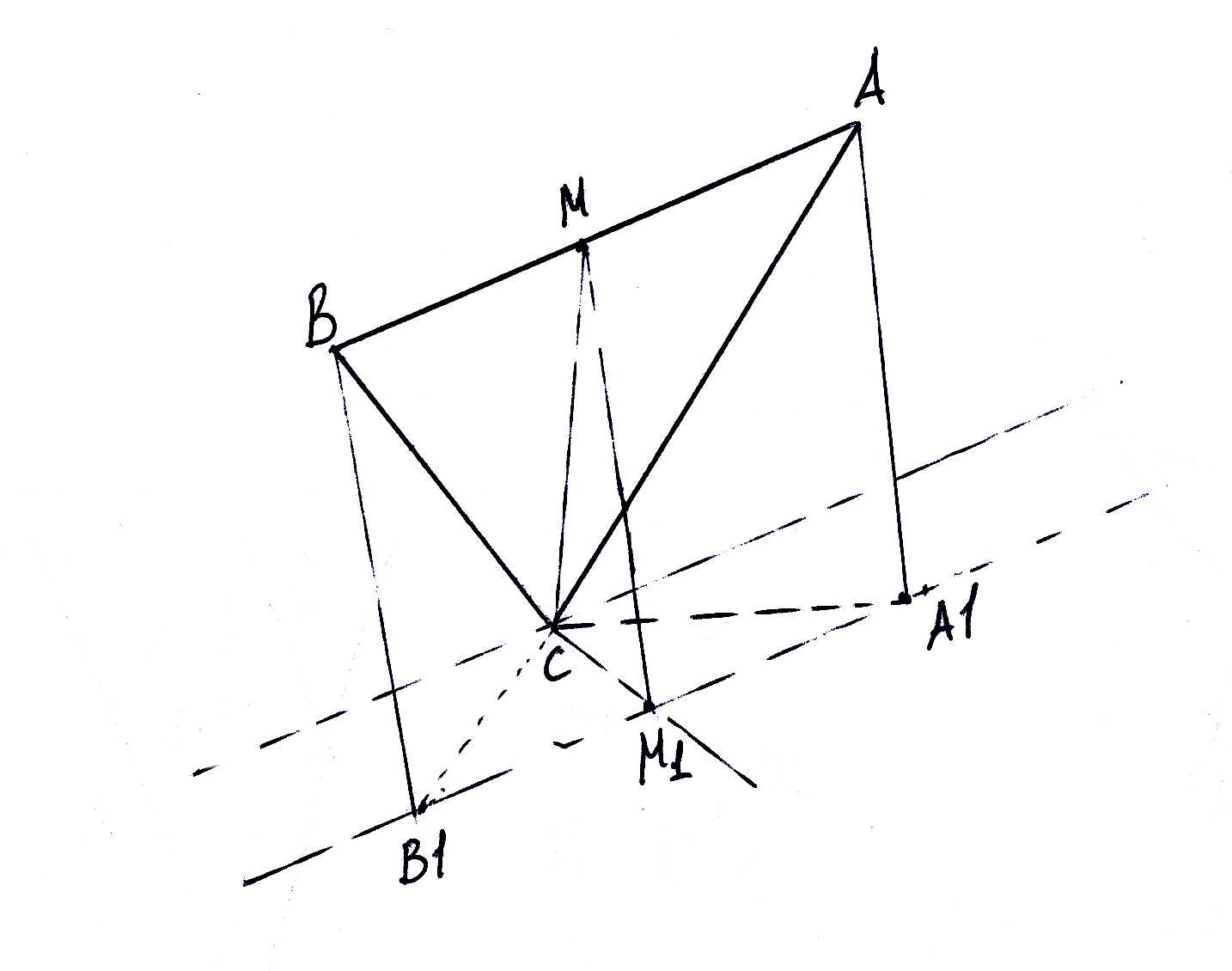