В основании пирамиды ABCD, все боковые ребра которой равны корень из 74 см, лежит прямоугольник со сторонами AB=8 см и BC=6 см. Найдите площадь сечения MSN, если оно перпендикулярно плоскости основании, а BM:MC=2:1

Решение:
В основании пирамиды SABCD, все боковые ребра которой равны  √74 см, лежит прямоугольник со сторонами AB=8 см и BC=6 см. Найдите площадь сечения MSN, если оно перпендикулярно плоскости основании, а BM:MC=2:1
Чтобы ответить на вопрос задачи,  необходимо знать высоту и основание сечения. т.е. SO и MN треугольника SMN.
В основании пирамиды прямоугольник.
Вокруг любого прямоугольника можно описать окружность.
Все четыре половины диагоналей являются радиусами описанной окружности и проекциями равных ребер пирамиды.
По т. Пифагора
АО=0,5 √(СВ²+АВ²)=5 см
SO=√(74-25)=7 cм
Высота сечения найдена. 
MN делит основание АВСD на две равные прямоугольные трапеции ( наверняка разберитесь, почему  равные-см. рисунок основания пирамиды) 
ВМ:СМ=2:1, ⇒ 
ВМ=4см, СМ=2см
Из прямоугольного треугольника МNH, где NH - перпендикуляр к СВ, найдем гипотенузу NM:
NН=AB=8см
NM=√(МН²+NH²)=√(64+4)=2√17см
Sсечения=SO*MN:2=0,5*7*2√17=7√17см²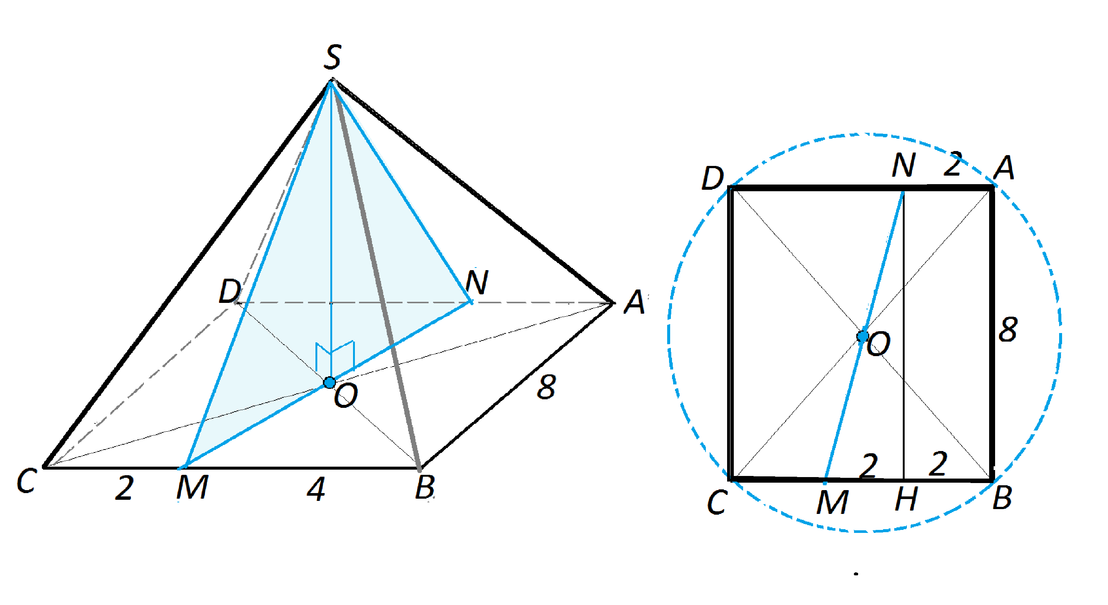