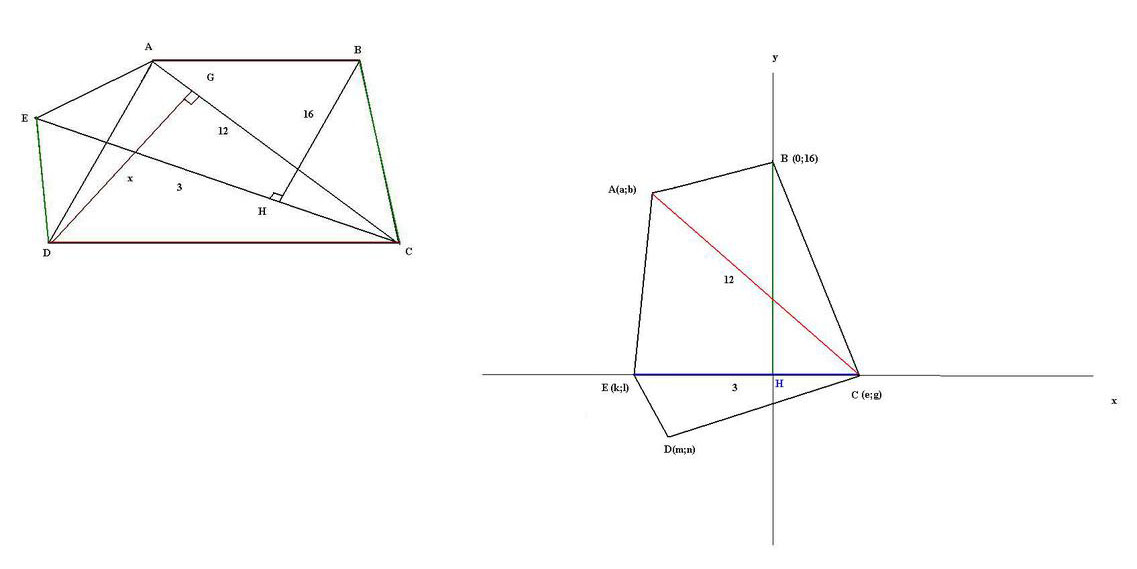
В пятиугольнике, АВ║CД, ДE║BC
АС=12, ЕС=3, от В до ЕС = 16, от Д до АС?

Решение:

Впишем наш пятиугольник в систему координат \( OXY \), так чтобы \( BH|| OY\\ EC|| OX \), где \( BH \) есть расстояние, тогда очевидно координата  \( B(0;16) \), тогда \( E(k;0)\\ C(e;0) \) где \( e;k \) координаты абсцисс соответствующих точек.    
Обозначим так же координаты \( A(a;b)\\ D(m;n) \), и  условимся что 
 \( m;n<0\\ a<0 \), так как иначе пятиугольник будет не выпуклый, что следует из анализа самой задачи.  
Так как \( EC=3\\ \sqrt{(e-k)^2}=3\\ |e-k|=3\\ \)
положим что  \( e=1\\ k=-2\\ \) что верно по условию, так как \( e<0 \).  То есть сама задача сводится на нахождение такой конструкций пятиугольника, что все компоненты будут верны, иными словами параллельность и длины.  
Так как мы знаем координаты точек  \( B(0;16) \ C(1;0) \), то его уравнение \( BC\\ 16x+y-16=0 \) по известной формуле по двум точкам.  
уравнение \( ED\\ -nx+(m+2)y-2n=0 \) 
а так как они параллельны, то выполняется условие 
 \( -\frac{-16}{n}=\frac{1}{m+2} \neq \frac{16}{2n} \) 
Вторую часть 
\( AB\\ (16-b)x+ay-16a=0\\\\ DC\\ -nx+(m-1)y+n=0 \) 
так же  \( \frac{16-b}{-n}=\frac{a}{m-1} \neq \frac{-16a}{n} \)
И выполняется условие 
\( (1-a)^2+b^2=144 \) то есть это длина отрезка \( AC \). 
из уравнения  
\( \frac{-16}{n}=\frac{1}{m+2}\\ n=-16(m+2) \)
так как \( n<0\\ m>-2 \), возьмем  \( m=-1 \), тогда \( n=-16 \), что верно по условию \( m,n<0 \)
Откуда получается система для второй точек координат 
 \( -32+2b=16a\\ (1-a)^2+b^2=144 \)
 из решения получаем 
 \( a=\frac{12\sqrt{61}-127}{65}\\ b=\frac{24(4\sqrt{61}+1)}{65} \) 
и все условию будут выполнены 
Теперь по формуле нахождения расстояние от точки до прямой  
уравнение \( AC \) 
  \( AC\\ 2*(4+\sqrt{61})+3y-2(4+\sqrt{61})=0 \) 
 координата точки \( D(-1;-16) \) 
 откуда расстояние равно 
 \( \frac{|-1*2(4+\sqrt{61})-3*16 - 2(4+\sqrt{61})|}{\sqrt{(2(4+\sqrt{61}))^2+3^2}}=4 \)