Точка М лежит на отрезке АВ. На окружности радиуса 32,5, проходящей через точки А и В, взята точка С, удаленная от точек А, М и И на расстояние 52,50 и 60 соответственно. Известно, что АВ>АС. Найдите площадь треугольника ВМС.

Решение:
Первый случай ( точка М находится правее точки N). I. Построение: Проводим радиусы OC и ОА. Проводим высоты ОН и СN. II. Расчет: 1) Найдем СN и ВN. ΔОHС ≈ ΔBNC по 2-ум углам (∢СОН =∢СВА, т.к вписанный ∢СВА и центральный ∢СОА опираются на дугу АС, т.е. ∢СВА в 2 раза < ∢СОА, а ∢СОН = 1/2 ∢СОА, т.к. высота в равнобедренном треугольнике является и медианой и биссектрисой; ∢ОНС = ∢ВNС).  ΔOНC: ОС = 32,5; НС = 26; ОН = 19,5. ΔВNС: СВ = 60; СN = ?; ВN = ?. ОС/СВ = НС/СN = ОН/ВN; 32,5/60 = 26/СN = 19,5/ВN; СN = 48, ВN = 36. 2) Найдем NМ. NМ = 14. 3) Найдем S ΔВМС. S ΔCNB = 1/2 · 36 · 48 = 864. S ΔCNM = 1/2 · 14 · 48 = 336. S ΔCMB = 864 - 336 =528. Второй случай - по аналогии. Только точка М находится левее точки N.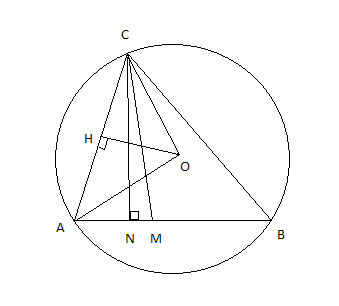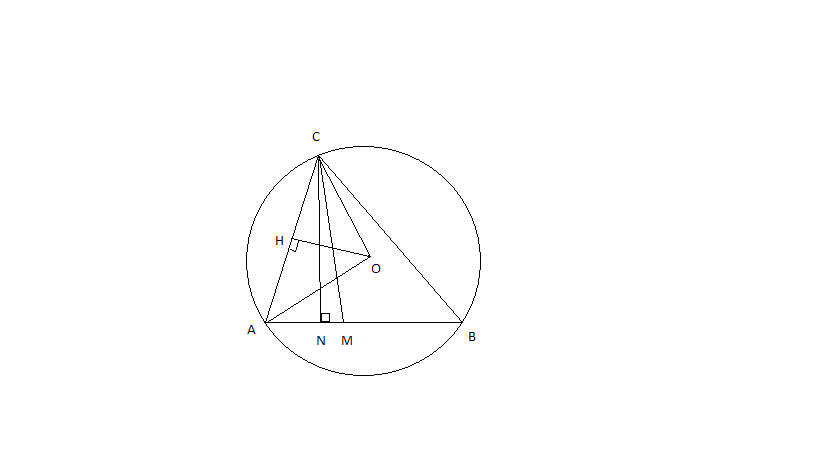