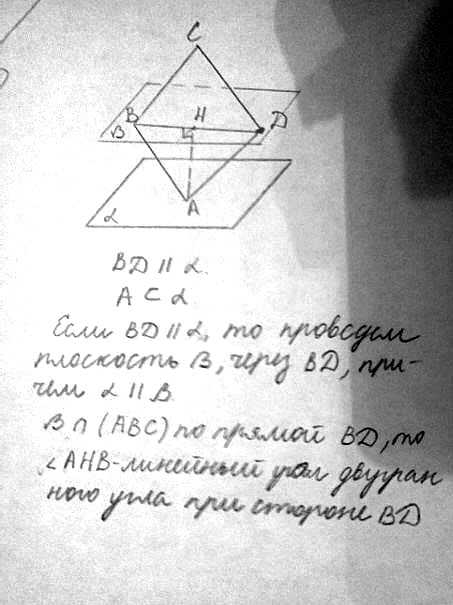
Вершина А ромба ABCD лежит в плоскости a, BD || а. Постройте линейный угол двугранного угла с гранями АВС и а
Решение:В плоскости а проведем прямую m, параллельную ВD
Опустим перпендикуляры из вершины А на диагональ ВD и на прямую m
Угол между этими перпендикулярами - это линейный угол двугранного угла с гранями АВС и а
В тетраэдере SABC угол BAC=90 градусов,SO-перпендикуляр к плоскости ABC, причем точка O лежит на отрезке АB. Постройте линейный угол двугранного угла SACO.
нам нужно построить угол при ребре АС
SO перпендикуляр к плоскости основания АВС.
По условию угол ВАС=90, Следовательно, АВ⊥АС (то есть ОА⊥АС)
Вы уже ведь даже говорите, что SA- наклонная, ОА - ее проекция. Следовательно, по т. О трех перпендикулярах SA⊥AC
Значит, угол SAO - линейный угол двугранного угла при ребре АС
И я не пойму, что вам не нравится.
Вам сказано не найти числовое значение этого угла. А построить.
Можно было бы и иначе
АС перпендикулярно АВ, SO- перпендикуляр к плоскости основания, то есть он перпендикулярен любой прямой в этой плоскости, то есть перпендикулярен и АС
Значит,
АС⊥АВ, АС⊥SO, значит, АС⊥SAB
Ну, и следовательно угол SAB искомый
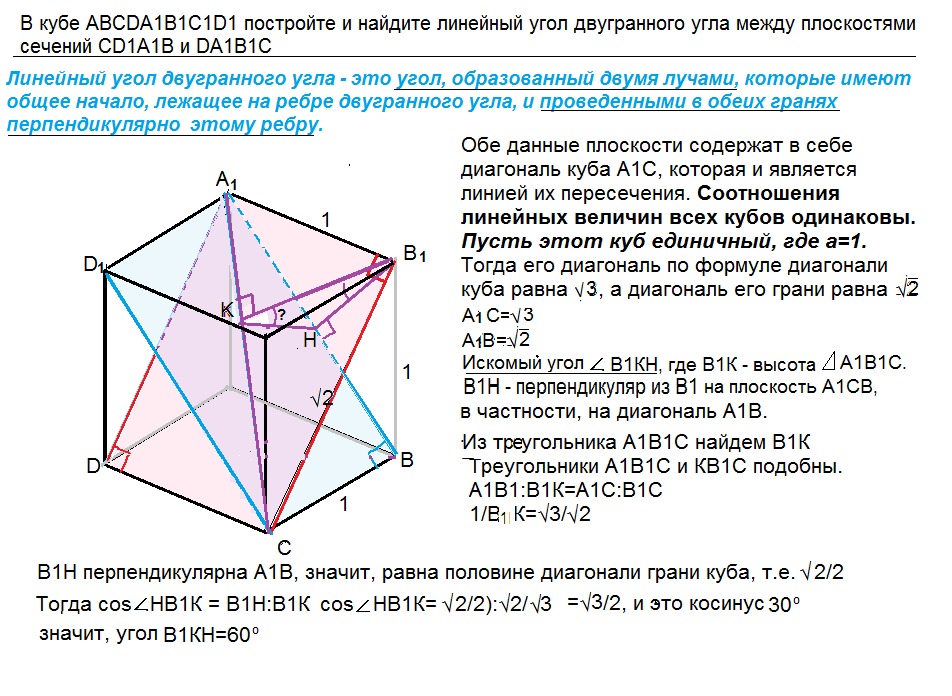
В кубе ABCDA1B1C1D1 постройте и найдите линейный угол двугранного угла между плоскостями сечений CD1A1B и DA1B1C
Определение: Двугранный угол – это фигура, образованная двумя полуплоскостями, исходящими из одной прямой.
Линейный угол двугранного угла - это угол, образованный двумя лучами, которые имеют общее начало, лежащее на ребре двугранного угла, и проведенными в обеих гранях перпендикулярно этому ребру.
Обе плоскости сечения содержат в себе диагональ куба А1С, которая является линией их пересечения.
Соотношение линейных величин у кубов одинаковы.
Пусть данный куб единичный, где его ребро равно 1.
Тогда его диагональ А1С по формуле диагонали куба равна √3, а диагональ его грани равна √2.
А1С=√3 А1В=√2
Искомый угол ∠В1КН, где В1К - высота треугольник аА1В1С.
В1Н - перпендикуляр из В1 на плоскость А1СВ, в частности, В1Н перпендикулярен А1В.
Из треугольник аА1В1С найдем В1К.
Треугольники А1В1С и КВ1С подобны.
А1В1: В1К=А1С: В1С
1/В1К=√3/√2
Грани куба - равные квадраты.
Диагонали квадрата перпендикулярны и точкой пересечения делятся пополам.
В1Н ⊥ А1В, ⇒ является половиной диагонали грани куба и равна ( √2):2
В1К ⊥ А1С, НК ⊥ А1С.
Треугольник В1НК - прямоугольный.
cos ∠ НВ1К=В1Н:В1К
cos ∠НВ1К=(√2/2):√2/√3=√3/2, и это косинус угла 30º.
Значит, угол В1КН, как второй острый угол прямоугольного треугольника, равен 90º-30º=60º
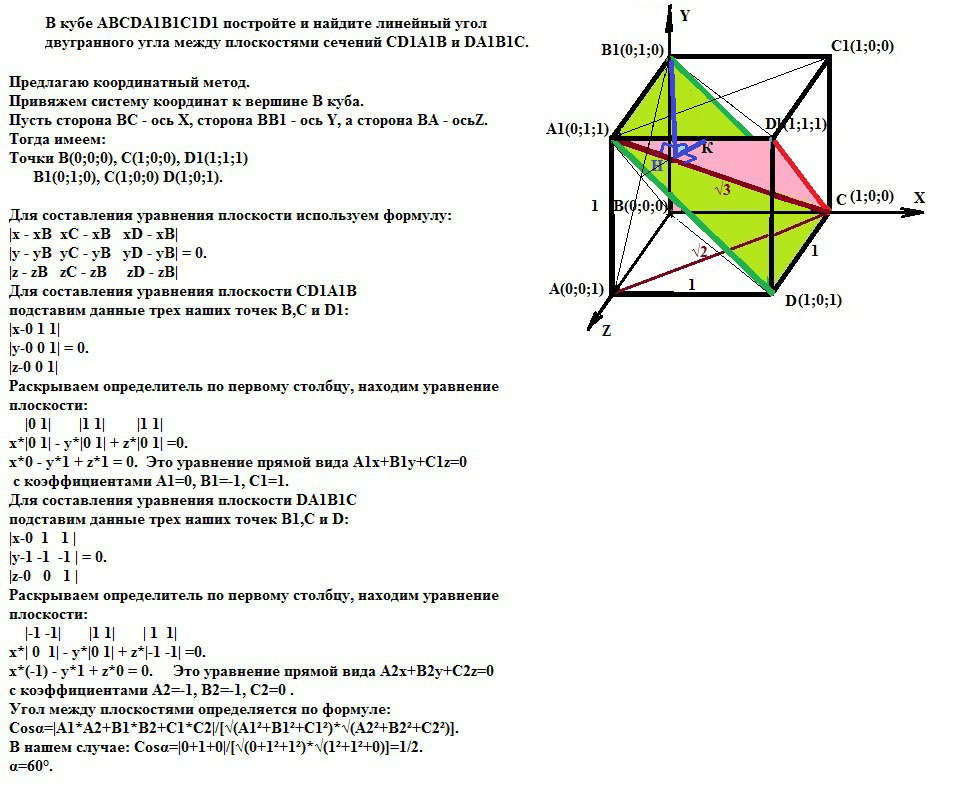
Предлагаю координатный метод.
Привяжем систему координат к вершине В куба.
Пусть сторона ВС - ось Х, сторона ВВ1 - ось Y, а сторона ВА - осьZ.
Тогда имеем:
Точки В(0;0;0), C(1;0;0), D1(1;1;1)
B1(0;1;0), C(1;0;0) D(1;0;1).
Для составления уравнения плоскости используем формулу:
|x - xB xC - xB xD - xB|
|y - yB yC - yB yD - yB| = 0.
|z - zB zC - zB zD - zB|
Для составления уравнения плоскости CD1A1B
подставим данные трех наших точек B,C и D1:
|х-0 1 1|
|y-0 0 1| = 0.
|z-0 0 1|
Раскрываем определитель по первому столбцу, находим уравнение плоскости:
|0 1| |1 1| |1 1|
х*|0 1| - y*|0 1| + z*|0 1| =0.
x*(0-0) - y*(1-0) + z*(1-0) = 0. Или
х*(0)-y*(-1)+z*(1)=0 Это уравнение прямой вида А1х+В1y+C1z=0 с коэффициентами А1=0, В1=-1, С1=1.
Для составления уравнения плоскости DA1B1С
подставим данные трех наших точек B1,C и D:
|х-0 1 1 |
|y-1 -1 -1 | = 0.
|z-0 0 1 |
Раскрываем определитель по первому столбцу, находим уравнение плоскости:
|-1 -1| |1 1| | 1 1|
х*| 0 1| - y*|0 1| + z*|-1 -1| =0.
x*(-1-0)) - y*(1-0) + z*(-1+1) = 0. Или
х*(-1)-y*(1)+z*(0)=0 Это уравнение прямой вида А2х+В2y+C2z=0 с коэффициентами А2=-1, В2=-1, С2=0.
Угол между плоскостями определяется по формуле:
Cosα=|A1*A2+B1*B2+C1*C2|/[√(A1²+B1²+C1²)*√(A2²+B2²+C2²)].
В нашем случае: Cosα=|0+1+0|/[√(0+1²+1²)*√(1²+1²+0)]=1/2.
α=60°.
Ответ: искомый угол равен 60°.