Две окружности с центрами О1 и О2, радиусы у которых равны пересекаются в точках M и N, через точку М проведена прямая параллельной О1О2 и пересекающая окружность с центром О2 в точке Д. Используя переллельный перенос докажите, что четырехугольник О1МДО2 является параллелограммом. ..

Решение:
О1М и О2Д - радиусы равных окружностей. следовательно, они равны. 
Опустив перпендикуляры Ма из М и  Дн из Д на прямую О1О2, получим равные между собой отрезки,  они равны е также высоте четырехугольника О1О2ДМ. Прямоугольные треугольники О1аМ и О2нД равны по гипотенузе и катету, и их основания лежат на одной прямой.
Сдвигая окружность О1 по прямой О1О2,  получим совмещение  О1 и О2, т.к.
МД || О1О2,
Совпадут и перпендикулярные отрезки между прямыми,  опущенные из точек пересечения радиусов с окружностью. 
Расстояние между их вершинами М и Д,  О1 и О2 равны.
Следовательно, МД=О1О2. 
Четырехугольник, в котором стороны попарно равны и параллельны, - параллелограмм
Четырехугольник О1МДО2 является параллелограммом, что и требовалось доказать.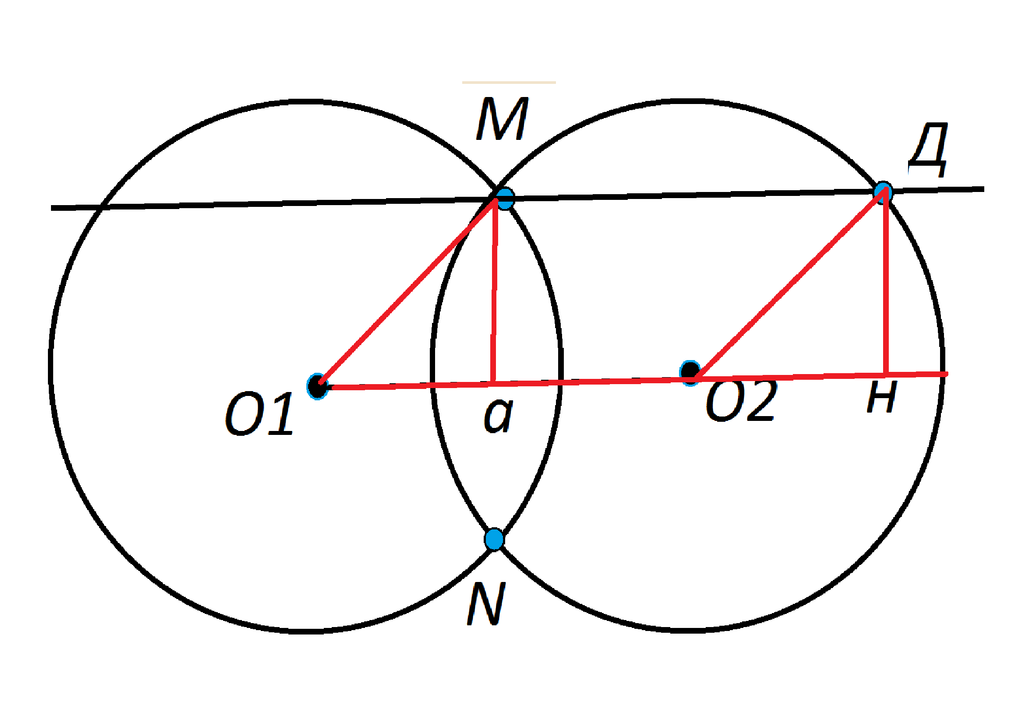