Дан пятиугольник KLMNP, в котором прямая KL параллельна прямой MN, прямая NP параллельна прямой LM, длина диагонали КМ равна 20, длина диагонали МР равна 16. Найдите расстояние от точки N до прямой КМ, если расстояние от точки L до прямой PM равно 15.

Решение:

Если достроить 5-угольник до параллелограмма (у него ведь пары сторон параллельны), то, вспомнив, что у треугольников с равными сторонами и равными высотами, проведенными к этим сторонам, площади равны, задача легко решается)
в условии даны два отрезка и перпендикуляры к ним -так и хочется рассмотреть треугольники с основаниями 20 и 16 (данными диагоналями)
но прежде нужно вспомнить, что в параллелограмме площадь треугольника, опирающегося на сторону параллелограмма, с вершиной, лежащей на противоположной стороне параллелограмма, равна половине площади параллелограмма!
интересно, что не важно ГДЕ на стороне лежит вершина треугольника!
т.е. Сначала нужно рассмотреть рисунок в рамочке)
это задача-основа для решения.  
а теперь становится очевидно, что площади треугольников, опирающихся на сторону (любую сторону) параллелограмма (LM, NM) с вершиной на противоположной стороне параллелограмма (и не важно где именно эта вершина, лишь бы она была на противоположной стороне. ))) просто равны.
. Равны половине площади параллелограмма
я высоты к сторонам параллелограмма строить не стала -они не нужны.
Н1 -высота параллелограмма к стороне LM
Н2 -высота параллелограмма к стороне NM
остальное очевидно из рисунка)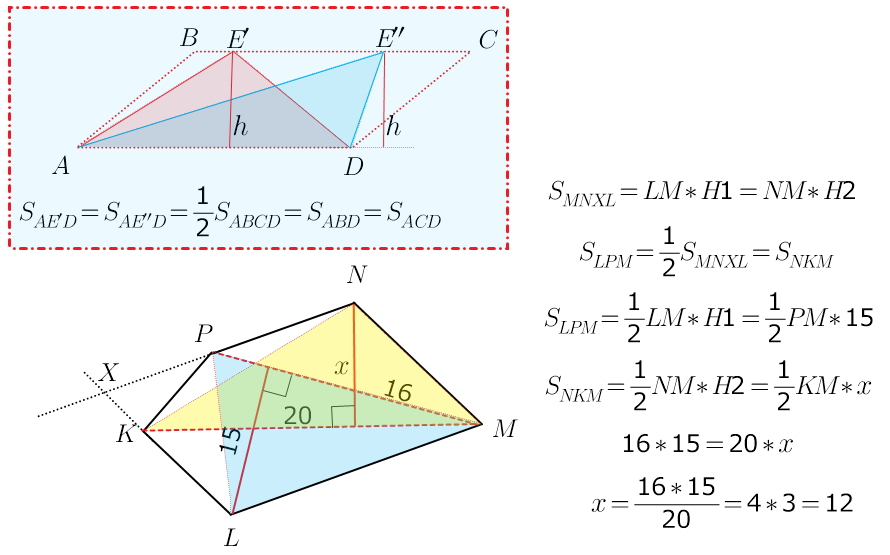