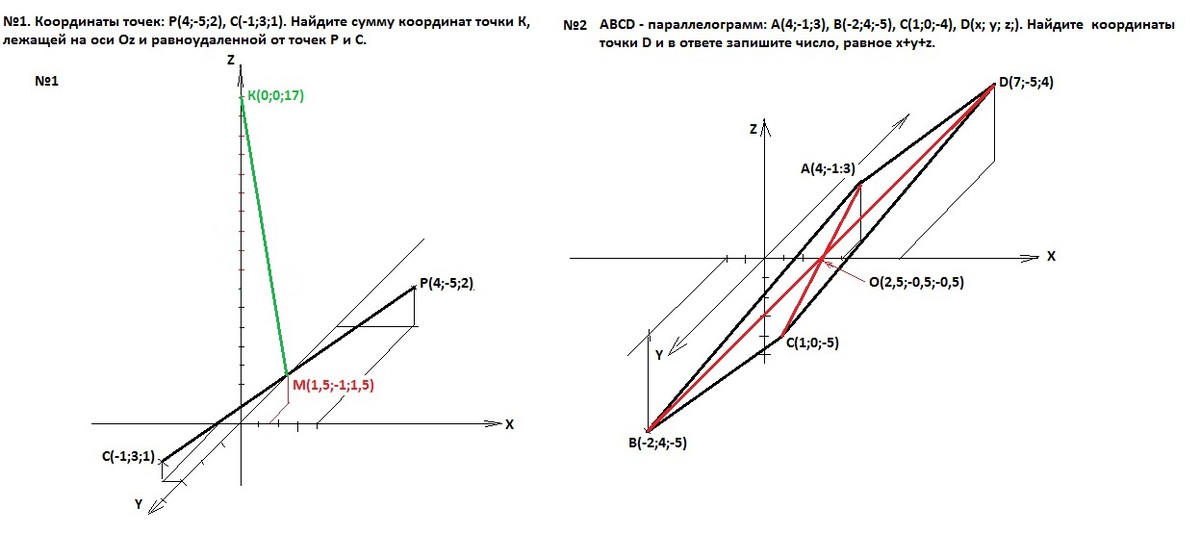
№1. Координаты точек: Р(4; -5;2), С(-1; 3; 1). Найдите сумму координат точки К, лежащей на оси Oz и равноудаленной от точек Р и С.
№2 ABCD - параллелограмм: А(4; -1; 3), В(-2; 4; -5), С(1; 0; -4), D(x; y; z;). Найдите координаты точки D и в ответе запишите число, равное x+y+z.

Решение:

№1. Надо через середину вектора РC провести плоскость, перпендикулярную РC и найти точку пересечения этой плоскости и оси Z. Точка пересечения будет очевидно равноудалена от точек Р и С.
Вектор РC{-5;8;-1} (из координат начала вычитаем координаты конца), его середина -
точка М(1,5;-1;1,5) (координаты середины отрезка PC находим по формуле
x=(x1+x2)/2, y=(y1+y2)/2, z=(z1+z2)/2).
Уравнение плоскости, проходящей через точку М(Хо;Yo;Zo) перпендикулярно вектору
PC{n1;n2;n3}, выражается формулой:
n1(X-Xo)+n2(Y-Yo)+n3(Z-Zo)=0.
В нашем случае: -5Х+7,5+8Y+8-Z+1,5=0 или 5Х-8Y+z-17=0.
Тогда точка К пересечения этой плоскости с осью 0z (х=0 и y=0) будет иметь координаты К(0;0;17).
Сумма координат этой точки равна 17.
Проверка: найдем модули векторов КС и КР. Вектор КС{1;3;16}, вектор КР{4;-5;15}.
Модули векторов: |КC|= √(1+9+256)=√266. |KP|=√(16+25+225)=√266. Итак, расстояния от точки К до точек С и Р равны.
№2. Чтобы найти координаты вершины D параллелограмма, надо найти точку О пересечения его диагоналей (а так как в параллелограмме диагонали точкой пересечения делятся пополам, надо найти середину вектора АС) и найти координаты вектора ВD по координатам его начала (точка В) и середины (точка О).
Итак, координаты точки О (середина отрезка АС) находим по формуле: x=(x1+x2)/2, y=(y1+y2)/2, z=(z1+z2)/2).
В нашем случае это О(2,5;-0,5;-0,5). Тогда координаты конца вектора ВD найдем по этой
же формуле, подставив известные значения точек В и О:
-2+Хd=5, 4+Yd=-1,5+Zd=-1. Xd=7, Yd=-5, Zd=4. Итак, имеем точку D(7;-5;4).
Тогда сумма координат этой точки равна 6.
Проверка: Вектора АВ и CD (также как и  BC и АD) должны быть равны по модулю и коллинеарны. Найдем координаты векторов:
AB={-6;5;-8}, CD{6;-5;8}. BC{3;-4;-1}, AD{3;-4;1} И их модули:
|AB|=√125, |CD|=√125. |BC|=√26, |AD|=√26. Итак, фигура АВСD - параллелограмм.