Диагонь правильной четырёхугольной призмы наклонена к плоскости основания под углом 60°. Найдите диагональ правильной четырёхугольной призмы наклонена к плоскости основания под углом 60°. Найдите площадь сечения, проходящего через сторону нижнего основания и противолежащую сторону верхнего основания,

Решение:
для начала построим диагональ..призмы...затем диагональ основания..получается прямоугольный треугольник ..так как угол наклона к плоскости 60, то автоматически (исходя из того что прямоугольный треугольник) другой угол равен 30.отсюда и правило: катет лежащий напротив угла в 30° равен половине гипотенузы..как раз диагональ основания лежит напротив этого угла..поэтому диагональ (гипотенуза) призмы равна 2*4√2 = 8√2 теперь найдем сторону квадрата.., так как диагональ равна  a√2 = 4√2, отсюда a = 4 из другого прямоугольника где 2 катета это высота призмы и сторона основания.. найдем эту высоту призмы: из пред. прямоугольного треугольника = по косинусу угла: cos 30 = x / 8√2, х = 4√6 найдем гипотенузу этого треугольника: 96 + 16 = (112) = 4√7 и вот почти все: теперь найдем площадь сечения(он же прямоугольник) S = a*b (a - сторона основания, b - диагональ боковой грани(та же гипотенуза)) = 4*4√7  = 16√7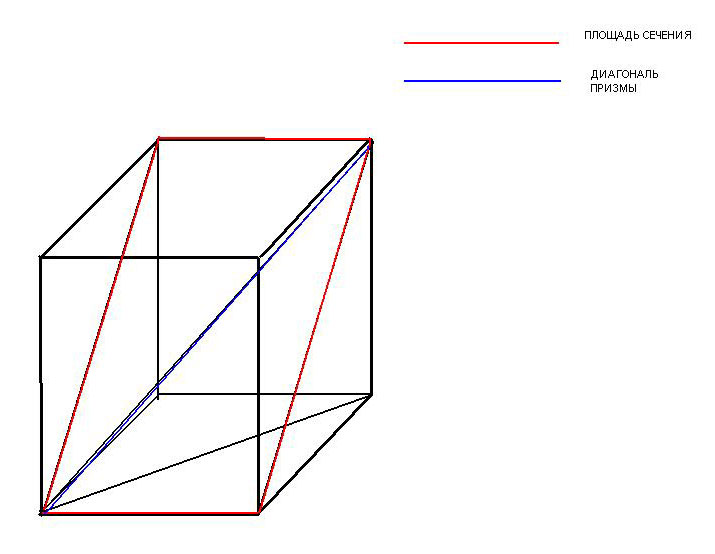