Дана прямоугольная трапеция ABCD (AD - большее основание, AB перпендикулярно AD). Площадь трапеции равна 150 корней из 3 сантиметров в квадрате, угол CDA = углу BCA = 60°. Найти диагональ АС.

Решение:
BCD+CDA=180 ACD=180-(60+60)=60 => треугольник ACD- равносторонний В треугольнике ABC угол BAC=30° , то есть сторона лежащая против угла 30° равна половине гипотенузы Пусть BC=x,  тогда AD=AC=CD=2x H=AB=AC*cos(30)=2x√3/2=x√3
s=(a+b)*h/2 150√3=(x+2x)x√3/2 300√3=3x^2√3 x^2=100=> x=10 то есть   AC=2x=20

Можно и без x и без тригонометрических функций: Площадь трапеции=1/2(ВС+АД)*АВ=150√3 Выразим эти три стороны чрез АС: Исходя из формулы сумм углов многоугольника, АСД действительно равносторонний треугольник т. к. угол ВАС = 30° (если АСД равносторонний и угол САД = 60°), то АС=2ВС, т. е. ВС=0,5*АС из равносторонности АД=АС, АВ будет высотой АСД и равно (из частной формулы для равностороннего треугольника) (√3/2)*АС⇒АВ=(√3/2)*АС Подставляем выделенное в формулу площади трапеции: ((0,5*АС+АС)/2)*(√3/2)*АС=150√3 (1,5АС)/2)*(√3/2)*АС=150√3 ((1,5√3)/4)*АС²=150√3 АС²=(150√3*4)/(1,5√3) АС=√(600/1,5)=√400=20

Диагональ равнобедренной трапеции перпендикулярна боковой стороне. Найти диагональ трапеции, если радиус описанной окружности равен 13см, а боковая сторона 10 см.

построй по заданию рисунок
видно, что боковая сторона(10 см)-нижнеее основание трапеции (гипотенуза=2R=2*13=26) и диагональ трапеции образуют прямоугольный треугольник
тогда по теореме Пифагора 
диагональ трапеции =√26^2-10^2= 24

Трапеция у нас равнобедренная, значит АВ=CD=10 или угол АВD=90°.
АD - диаметр. AD = 2R = 26 из прямоугольного треугольника АВD по теореме Пифагора определим катет BD:
BD^2=AD^2-AB^2=26^2-10^2=576
BD=24

---

Трапеция ABCD- равнобедренная, значит,
АВ=CD=10 или угол АВD = 90°.
АD - диаметр.
AD = 2R = 26 из прямоугольного треугольника АВD по теореме Пифагора определим катет BD:
BD^2=AD^2-AB^2=26^2-10^2=576
BD=24
Ответ: 24

В равнобедренной трапеции ABCD основания AD и BC соответственно равны 18 см и 12 см. Боковая сторона образует угол 30° с основанием. Найти диагональ трапеции.

1. Раз надо половину - проводим биссектрису )) Получился египетский треугольник (5,12,13) (точнее, их получилось 2 ) Отсюда, если угол Ф, то
sin(Ф/2) = 5/13; cos(Ф/2) = 12/13; tg(Ф/2) = 5/12.
2. Опускаем высоты из В и С на AD, и видим по бокам 2 РАВНОБЕРЕННЫХ прямоугольных треугольника - у них гипотенузы 2, а катеты, которые - куски AD, равны корень(2). То есть углы 45 и, само собой,135°.
3. Делаем то же самое, но уже только с одной стороны, потому что мы уже знаем (в предыдущем пункте считали ), что отрезок от D до основания высоты из С на AD, равен полуразности оснований, то есть, в данном случае, (18-12)/2 = 3. Поэтому высота равна 3*(корень(3)/3) = корень(3)
а диагональ находится из треугольника, образованного ДРУГОЙ высотой - из В на AD и отрезком 18 - 3 = 15 (между прочим, это равно средней линии.
d = корень(15^2 + (корень(3))^2) = 2*корень(57)

Основания равнобедренной трапеции равны 3м и 8м, а угол при основании равен 60 градусам. Найти диагональ трапеции

Смотри рисунок во вложении.  
Проведем высоты BH и AH1.
DH1 = HC, так как в равнобедренной трапеции AD=BC, а AH1=BH, как высоты.
еще HH1 = AB (из прямоугольника ABHH1)
Тогда HC = (ВС-AB)/2 = 2,5 
Тогда в треугольнике BHC: cos C = HC/BC. Следовательно BC = HC/ cos60 = 5
По теореме косинусов
BD^2 = DC^2 + BC^2 - 2* BC* DC * cos 60 = 64 + 25 - 8*5 = 64 + 25 - 40= 49
BD = 7
Ответ: 7.

Диагональ равна 7 м решение в приложении.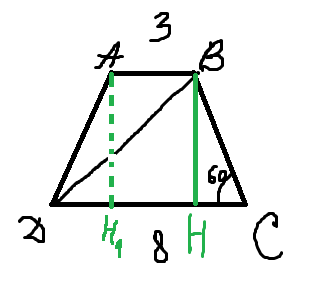