Основание пирамиды - ромб с диагоналями 30 см и 40 см.Вершины


Главная Научный калькулятор
Меню Алгебра Геометрия Основные понятия Аксиомы планиметрии Углы Перпендикулярные и параллельные прямые Перпендикуляр и наклонная Круг (окружность) Треугольник Четырехугольник Параллелограмм Трапеция Многоугольники Основные понятия стереометрии Аксиомы стереометрии Прямые в пространстве Пересекающиеся прямые Параллельные прямые Скрещивающиеся прямые Прямая и плоскость в пространстве Перпендикулярность прямой и плоскости Параллельность прямой и плоскости Угол между прямой и плоскостью Теорема о трех перпендикулярах Формула двойного проектирования Плоскости в пространстве Пересекающиеся плоскости Параллельность плоскостей Перпендикулярность плоскостей Площадь проекции плоской фигуры на плоскость Многогранники: Пирамида Призма Тела вращения: Цилиндр Конус Шар (Сфера) Объем тел вращения Задачи по геометрии Примеры решений Вспомогательные материалы: Таблицы Брадиса Исследование функций Асимптоты. Первая производная. Вторая производная. Тригонометрия Тригонометрические неравенства Преобразования графиков	Треугольник : Равнобедренный треугольник : Прямоугольный треугольник : Четырехугольник : Параллелограмм : Ромб : Прямоугольник : Трапеция : Многоугольники : Круг и окружность : Прямые и плоскости : Пирамида : Пространственная система координат : Цилиндр : Конус : Углы : Призма : Параллелепипед : Сфера и Шар Основание пирамиды - ромб с диагоналями 30 см и 40 см. Вершины пирамиды удалены со сторонами основания на 13 см. Найдите высоту пирамиды Решение: Основание пирамиды - ромб. Диагонали ромба взаимно перпендикулярны и в точке пересечения делятся пополам. Тогда из прямоугольного треугольника, образованного половинами диагоналей (катеты) и стороной ромба (гипотенуза) по Пифагору находим сторону ромба: DC = √(15² + 20²) = √625 =25см. Площадь ромба (основания) равна полупроизведению его диагоналей, то есть Sр=(1/2)3040 = 600см². С другой стороны, площадь ромба равна произведению высоты на сторону, откуда высота ромба равна 600:25 = 24см. Точка пересечения диагоналей делит пополам и высоту ромба, тогда из прямоугольного треугольника, образованного половиной высоты ромба, высотой пирамиды (катеты) и апофемой грани пирамиды (гипотенуза) по Пифагору находим высоту пирамиды. Н = √(13² -12²) = √25 = 5см. Ответ: высота пирамиды равна 5см. 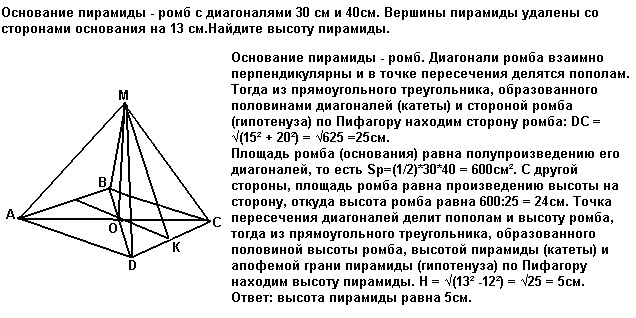Основанием пирамиды служит ромб, сторона которого равна a, а острый угол 60⁰. Боковые грани наклонены к основанию под углом 45⁰. Найдите высоту пирамиды и площадь ее боковой поверхности. Боковые грани пирамиды, в основании которой ромб, равные треугольники. Если они наклонены под равным углом к основанию, то проекции их равных высот также равны и потому равны радиусу вписанной в ромб окружности. Центр этой окружности - точка О пересечения диагоналей ромба. 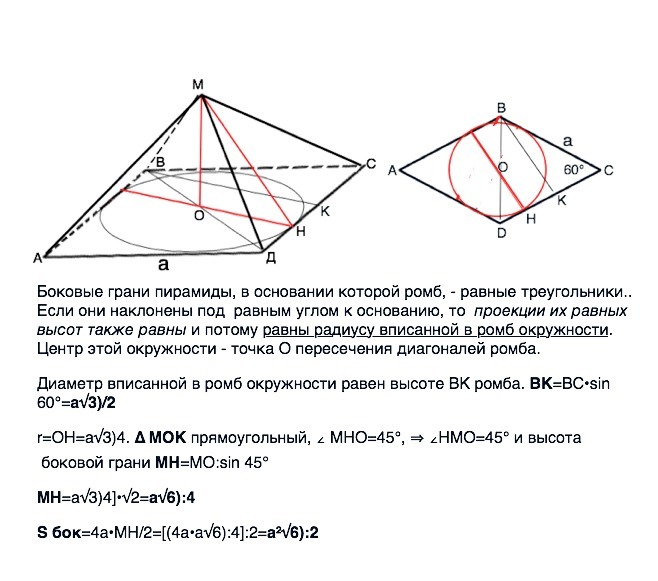Диаметр вписанной в ромб окружности равен высоте ВК ромба. ВК=ВС•sin 60°=a√3)/2 r=ОН=a√3)4. ∆ МОК прямоугольный, ∠ МНО=45°, ⇒ ∠НМО=45° и высота боковой грани МН=МО:sin 45° МН=a√3)4]•√2=a√6):4 S бок=4а•MH/2=[(4a•a√6):4]:2=a²√6):2 Основанием пирамиды служит ромб с диагоналями 6см и 8см. Высота проходит через точку пересечения диагоналей ромба лежащего в основании пирамиды и равна 1см, Определить боковую поверхность пирамиды. Диагонали точкой пересечения делятся пополам и угол между ними прямой. Значит сторона ромба = корень из (9+16) = корень из 25 = 5 апофема = корень из (1+6,25) = корень из 7,25 (6,25 - квадрат числа 2,5, а это - половина стороны основания = высоте треугольников составляющих основание) Площать боковой поверхности = 0,5периметр основания (20) апофему (корень из 7,25) = 10 корней из 7,25 Основанием пирамиды служит ромб со стороной 6 см и острым углом 30. Все двугранные углы при основании равны. Боковая поверхность пирамиды равна 36. Найти величину двугранного угла при основании A =12 см ;S бок =36 h₁ = Hосн =a/2 =6 см /2 =3 см (катет против угла 30°) ; r = h₁/2 =3/2 см. Sбок =40,5ah =2ar/cosβ =(263/2)/cosβ =18/cosβ; * * * h - апофема * * * 36 =18/cosβ⇒cosβ =18/36 =1/2. β =60°. - проще - Если все двугранные углы при основании равны, то : Sосн =Sбокcosβ ; a² sinα = Sбокcosβ ; cosβ = a² sinα/Sбок =6²sin30°/36 =1/2 ; β = 60* Основанием пирамиды служит ромб с острым углом, равным 60. Сторона ромба и высота пирамиды равны а, основание высоты пирамиды совпадает с вершиной острого угла ромба. Найдите площадь боковой поверхности пирамиды Площадь боковой поверхности пирамиды состоит из площади двух пар треугольников S=2S_ABN+2S_BCN ABN прямоугольный с катетами, равными а, 2S_ABN=\( a^{2} \) BN=\( a \sqrt{2} \) NC=\( \sqrt{AN^{2}+AC^{2}} \) AC=a\( \sqrt{2+2cos \alpha } =a \sqrt{3} \) NC=\( \sqrt{ a^{2}+3 a^{2} } =2a \) По формуле Герона S_BCN=\( \sqrt{p(p-BC)(p-CN)(p-BN)} = \) p=(BC+CN+BN)/2=a(1+2+√2)/2=a(3+√2)/2 S_BCN=\( \sqrt{ \frac{a^4}{16}(3+ \sqrt{2})(3+ \sqrt{2}-2 \sqrt{2})(3+ \sqrt{2}-4)(3+ \sqrt{2}-2) }= \) =\( \frac{a^2}{4} \sqrt{(3+ \sqrt{2})(1+ \sqrt{2})( \sqrt{2}-1)(3- \sqrt{2}) } = \frac{a^2 \sqrt{7} }{4} \) 2S_BCN=\( \frac{a^2 \sqrt{7} }{2} \) S=\( a^{2} +\frac{a^2 \sqrt{7} }{2} = a^{2} \frac{2+ \sqrt{7} }{2} \) ≈2,32a² Основание пирамиды - ромб с диагоналями 12см и 16 см. Объем равен 480см в кубе. Найти площади диагональных сечений Площадь ромба равна S = ½ a* b, где a,b - диагонали ромба S= ½ * 12* 16 = 96 см² Объем пирамиды равен: V = ⅓ Sh, найдем отсюда высоту пирамиды h = 3V/h, h = 3 * 480/96 = 15 см Диагональными сечениями пирамиды будут треугольники, найдем их площади S = ½ a* h S1 = ½ * 12 * 15 = 90 cм² площадь первого сечения S2 = ½ * 16 * 15 = 120 см²площадь второго сечения так как площадь ромба равна S=1/2ab, где a и b - диагонали ромба, то S=1/21216=96см² Объем пирамиды равен V=1/3Sh, отсюда найдем высоту пирамиды h=3V/S, h=3480/96=15см так как диагональные сечения - треугольники, то их площади равны S=1/2ah S₁=1/21215=90cм² первое сечение S₂=1/21615=120см² второе сечение Основание пирамиды - ромб с тупым углом α. Все двугранные углы при основании пирамиды равны β. Найдите площадь полной поверхности пирамиды, если её высота равна H. найдем высоту боковой грани H’=H/sinβ* найдем половину высоты основания h/2=H/tgβ => высота основания h=2H/tgβ угол между высотой основания (опущенной из вершины)и стороной основания а равен (α-90), тогда сторона основания равна а=h/cos(α-90)=*2H/[tgβcos(α-90)] S осн.** =ah=2H/[tgβcos(α-90)]2H/tgβ=(2H/tgβ)^21/cos(a-90) S бок. Пов=4(1/2aH’)=2H/sinβ*2H/[tgβcos(α-90)] Sполн. =S осн. +S бок. Пов=** =(2H/tgβ)^21/cos(a-90)+2H/sinβ 2H/[tgβcos(α-90)]= =(2H)^2/cos(a-90)(1/tgβ)^2+1/sinβ * 1/tgβ)= =(2H)^2/cos(a-90)(1/tgβ)^2+1/[sinβ cos β/cos β]* 1/tgβ)= =(2H)^2/cos(a-90)(1/tgβ)^2+1/cos β 1/(tgβ)^2)= =(2H)^2/[cos(a-90)(tgβ)^2](1+1/cos β) Основание пирамиды - ромб со стороной 16 см и острым углом 60°. Двугранные углы при основании пирамиды также равны 60 градусам. Вычислите площадь полной поверхности пирамиды. Если грани равнонаклонены, то в основание пирамиды можно вписать окружность (основание при этом - любой выпуклый многоугольник, тут все дело в том, что высота пирамиды "видна" из основания апофемы любой грани под одинаковым углом. Поэтому равны все апофемы и все их проекции, то есть в основании есть точка, равноудаленная от всех сторон. "Видна" означает, что все прямоугольные треугольники, составленные из высоты пирамиды, любой апофемы и её проекции на основание, имеют одинаковый острый угол, противолежащий общему катету, которым и является высота пирамиды. Поэтому эти треугольники все равны между собой). Поэтому шаблонное решение такой задачи - вычислить радиус вписанной окружности в ромб, а апофема будет в 2 раза больше (потому что угол между ними 60°), то есть равна диаметру вписанной окружности. При этом очевидно, что диаметр окружности - это высота ромба (когда окружность касается 2 параллельных прямых, её диаметр равен расстоянию между прямыми). То есть сторона, умноженная на sin(60). Итак, апофема равна 8корень(3), радиус вписанной окружности 4корень(3). Периметр ромба 64, поэтому площадь основания 644корень(3)/2, а площадь боковой поверхности 648корень(3)/2, и складываем. Получаем 384корень(3). Другой способ решения - основание можно рассматривать как "сумму ортогональных проекций граней", а поскольку грани равнонаклонены, Sboccos(Ф) = Sosn. cos(Ф) = 1/2, то есть площадь боковой поверхности в 2 раза больше площади основания. А площадь основания считается как 16^2sin(А), А - острый угол ромба. Полная площадь 316^2корень(3)/2 = 384корень(3) Основание пирамиды - ромб, один из углов которого 60°. Каждая боковая грань образует с плоскостью основания угол, равный 30°. Найдите площадь основания пирамиды, если высота пирамиды равна 6 см. Обозначим пирамиду АВСДS(смотри рисунок). Проведём высоту ОК в треугольнике АОД. Найдём её значение через тангенс угла наклона грани и высоту пирамиды. Прямоугольные треугольники ОКД и АОД-подобны по по острому углу АДВ. Он равен 60°, поскольку ВД-биссектриса угла АВС=120. Находим АО и ОД, затем площадь треугольника АОД, ромб состоит из четырёх таких треугольников. Ответ площадь основания равна 288корней из3.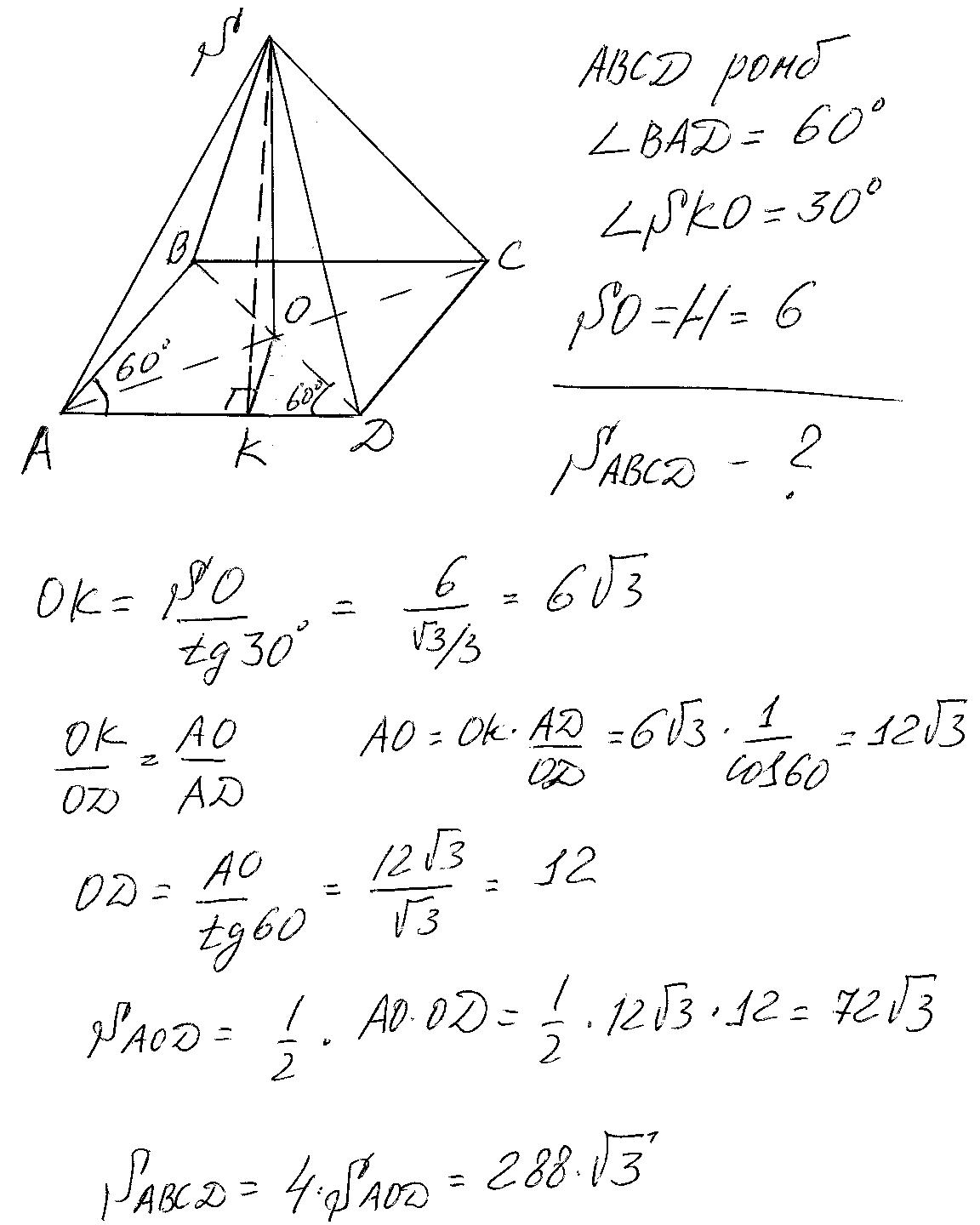 Основание пирамиды - ромб со стороной 16см и углом 30°. Все двугранные углы при ребрах основания составляют 60°. Найти объем пирамиды. Основание пирамиды - ромб со стороной 16см и углом 30°. Все двугранные углы при ребрах основания составляют 60°. Найти объем пирамиды. - Если все грани наклонены к основанию под равным углом, основание О высоты КО пирамиды находится в центре вписанной в основание окружности. Высота ВЕ ромба в основании равна половине его стороны, т.к. Противолежит углу 30°. ВЕ=16:2=8 Высоту КО пирамиды найдем из прямоугольного треугольника КОМ Диаметр вписанной окружности НМ равен высоте ромба ( основания)=8см Отрезок ОМ равен радиусу вписанной окружности ( половине высоты ромба) и равен 4 см угол КМО=60°⇒угол ОКМ=30° КО=ОМ:tg (30°)=4√3 *V=SH:3* S=АВМЕ=168=128 V=(1284√3):3=512√3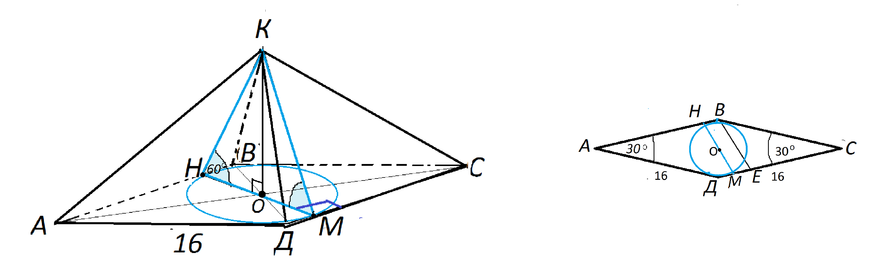* Основание пирамиды - ромб с периметром 40 см и площадью 60см в квадрате. Все двугранные углы при основании пирамиды равны 60 градусам. Найдите объем пирамиды Т. К. Все ребра наклонены к плоскости основания под одним углом, то высота падает в центр вписанной окружности диаметр окружности МК=высоте ромба ВН = 60/(40/4)=6 см радиус ОМ=6/2=3 cm Высота пирамиды SO=3tg60=3√3 cm V=1/3SоснSO=1/3603√3=60√3 cm³ 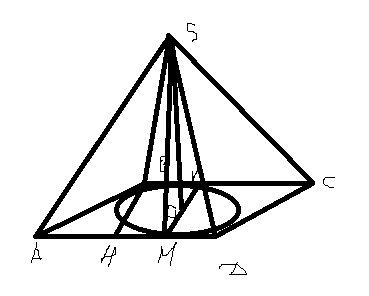Основание пирамиды - ромб с углом 30°). Все двугранные углы при ребрах основания составляют 60 °, Найти V, если высота пирамиды 3√3 см. Дано: AB=BC=CD=AD (ABCD _ромб), ∠A =30° ; ∠SEO =∠SFO=∠SMO=∠SNO = α =60°,SO=3√3. E∈[AB], F∈[BC], M ∈[AB],N ∈[CD]. - V - V =(1/3)Sосн H =(1/3)Sосн 3√3 = √3Sосн. Пусть основания высоты пирамиды точка O: * * * SO⊥ (ABCD), O ∈ (ABCD). * * * Если все двугранные углы при ребрах основания составляют равные углы (как в данном примере α=60°), то высота пирамиды проходит через центр окружности вписанной в основании (здесь ромб ). [[ Прямоугольные треугольники SEO, SFO,SMO и SNO равны по общим катетом SO и острым углам ∠SEO =∠SFO=∠SMO=∠SNO. ⇒EO =FO=MO=NO =r и SE,SF, SM, SN равные апофемы. ]] EF⊥ AD ; MN ⊥BC * * * Рассмотрим ΔESF: треугольник равносторонний ∠SEO =∠SFO=60°. SO =(a√3)/2= (EF√3)/2. 3√3 =(EF√3)/2⇒ EF = 6. Проведем BH ⊥AD. Ясно BH =EF =6. Из ΔABH: BH =AB/2 (катет против угла ∠A =30°) ⇒AB=2BH. Sосн =ADBH =ABBH =2BHBH =2BH² =26² =72. * * или Sосн =ABADsin∠A =AB²sin∠A * * V =√3Sосн =72√3. Основание пирамиды - ромб с острым углом 30°, высота пирамиды равна h, а каждая из боковых граней составляет с плоскостью основания угол 60°. Найдите полную поверхность пирамиды. Применены: свойство катета против угла в 30°, формула площади ромба, формула площади боковой поверхности пирамиды Пусть K вершина пирамиды, основание ABCD_ромб ; ∠BAD=30°; KO ⊥(ABCD), KO =h (высота пирамиды) ; OE ⊥ AD ; ∠KEO =60°. E ∈ AD - Sпол - Sпол = Sосн + Sбок. Все грани с плоскостью основания составляют равны углы (в данном случае 60°), значит высота пирамиды проходит через центр O окружности вписанной в основании ABCD. Через точку O проведем прямую, перпендикулярную AD (BC), которая пересекает сторону AD допустим в точке E, а сторону BC в точке F. KE и KF будут апофемы соответственно боковых граней AKD и BKC. Из OE ⊥ AD⇒OE ⊥ KE (теорема трех перпендикуляров). Треугольник EKF_равносторонний: (∠KEO=∠KFO=60°). Поэтому KE=KF=EF \|\| =2OE =2r\|\|. Из ΔKOE: KO =KE√3/2 ⇒KE=2KO/√3 =2h/√3. KE=KF=EF =2h/√3. Найдем сторону основания. Из вершины B опускаем перпендикуляр BN на AD. EF =BN =AB/2 (катет против угла 30°)⇒ AB=2EF. - Sосн =ABBN =2EFEF =2EF². Sбок=4(1/2)ADKE=2ADKE =2ABKE =22EFKE =4EF². Sпол = Sосн + Sбок =2EF²+4EF² =6EF²=6(2h/√3)² =(6*4/3)h²=8h². ответ: 8h².