найдите площадь прямоугольного треугольника


Главная Научный калькулятор
Меню Алгебра Геометрия Основные понятия Аксиомы планиметрии Углы Перпендикулярные и параллельные прямые Перпендикуляр и наклонная Круг (окружность) Треугольник Четырехугольник Параллелограмм Трапеция Многоугольники Основные понятия стереометрии Аксиомы стереометрии Прямые в пространстве Пересекающиеся прямые Параллельные прямые Скрещивающиеся прямые Прямая и плоскость в пространстве Перпендикулярность прямой и плоскости Параллельность прямой и плоскости Угол между прямой и плоскостью Теорема о трех перпендикулярах Формула двойного проектирования Плоскости в пространстве Пересекающиеся плоскости Параллельность плоскостей Перпендикулярность плоскостей Площадь проекции плоской фигуры на плоскость Многогранники: Пирамида Призма Тела вращения: Цилиндр Конус Шар (Сфера) Объем тел вращения Задачи по геометрии Примеры решений Вспомогательные материалы: Таблицы Брадиса Исследование функций Асимптоты. Первая производная. Вторая производная. Тригонометрия Тригонометрические неравенства Преобразования графиков	Треугольник : Равнобедренный треугольник : Прямоугольный треугольник : Четырехугольник : Параллелограмм : Ромб : Прямоугольник : Трапеция : Многоугольники : Круг и окружность : Прямые и плоскости : Пирамида : Пространственная система координат : Цилиндр : Конус : Углы : Призма : Параллелепипед : Сфера и Шар Найдите площадь прямоугольного треугольника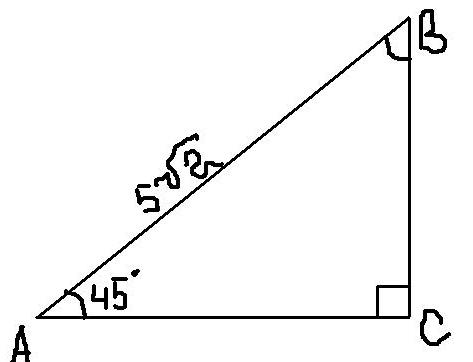 Решение: A = 45°, ‹ C = 90°значит ‹ В = 180°- ‹ A - ‹ C = 180° - 90°- 45°= 45° два угла треугольника равны, значит он равнобедренный AС=BC из теоремы Пифагора AC^2+BC^2=AB^2= 5√2 2AC^2=5√2 AC²=25 АС=ВС=5 Площадь прямоугольного треугольника равна половине произведения катетов S=AСВС/2 S=55/2=25/2=12.5 Найдите площадь прямоугольного треугольника, если гипотенуза его равна 40см а острый угол 60° Треугольник АВС, где угол В-прямой. Угол А=60°, тогда угол С=30°, гипотенуза равна 40 см. Катет, лежащий против угла в 30° равен половине длины гипотенузы, т. Е 20см. по теореме Пифагора 40^2-20^2=1600-400=1200 второй катет равен корню квадратному из 1200 1200=3400=20корень из 3 площадь треугольника равна 1/2 произведения катетов (первый катет 20см, а второй катет - 20 корень из 3) S=1/22020 корень из 3 S=200 корень из 3(см2) Второй острый угол будет равен 90-60=30 (теорема об углах треугольника. ), катет, лежащий против угла в 30°, равен половине гипотенузе=40:2=20, по теореме Пифагора находим второй катет= 40^2-20^2=1200, извлекаем корень, второй катет равен 20 корней из трех, площадь равно полупроизведению катетов, т.е. 20 умножить на 20 корней из 3 и поделить на два, будет 200 корней из трех. Треугольник АВС, где угол В-прямой. Угол А=60°, тогда угол С=30°, гипотенуза равна 40 см. Катет, лежащий против угла в 30° равен половине длины гипотенузы, т. Е 20см. по теореме Пифагора 40^2-20^2=1600-400=1200 второй катет равен корню квадратному из 1200 1200=3400=20корень из 3 площадь треугольника равна 1/2 произведения катетов (первый катет 20см, а второй катет - 20 корень из 3) S=1/22020 корень из 3S=200 корень из 3(см2) 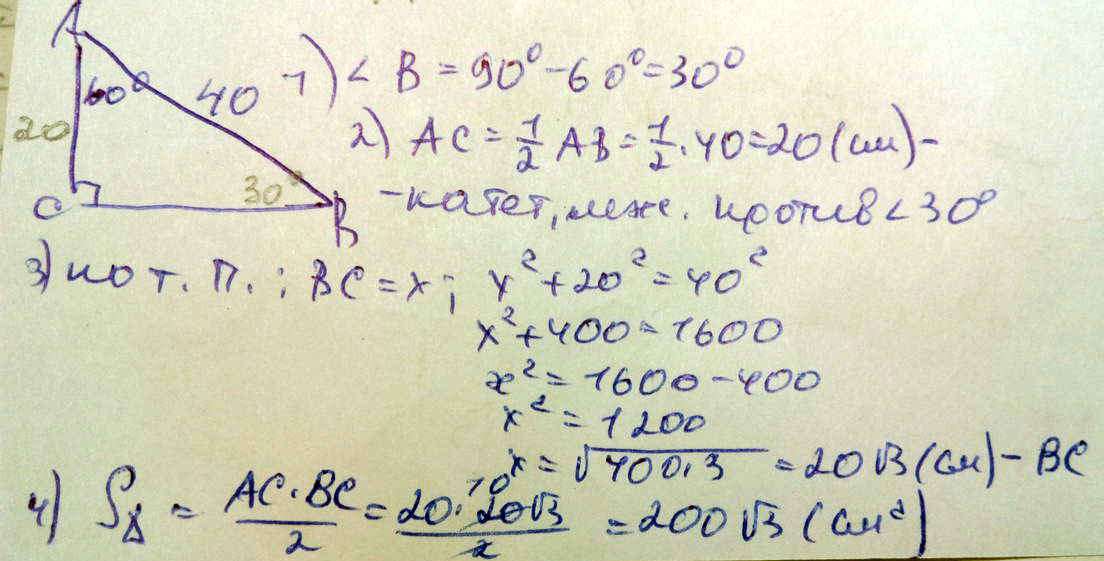Найдите площадь прямоугольного треугольника, если один из его катетов равен 12 см, а гипотенуза равна 13 см. s = a * b / 2 a - катет b - катет a = 12 b^2 = 13^2 - 12^2 b^2 = 169 - 144 b^2 = 25 b = 5 S = 5 * 12 / 2 S = 30 Найдем 2 катет. AB^2=AC^2-BC^2 AB^2=13^2-12^2 AB^2=169-144 AB=5 S=1/2 * AB * BC S=1/2 * 5 * 12 S=30 cm^2 Ответ: S=30 cm^2 Найдите площадь прямоугольного треугольника, если гипотенуза = 8, а один из острых углов = 60° Площадь прямоугольного треугольника измеряется как половина умножения его катетов, то чтобы найти его катеты, нужно воспользоваться теоремой Пифагора. А если один угол ровняется 60° то второй ровняется 30°, а сторона какая лежит напротив угла в 30 ровняется половине гипотенузы, значит одна сторона ровнется 4 см. С теоремы пифогора вырозим вторую сторону х в квадратке=64см2-16см2, вторая стора ровняется корню из 48)) тогда площадь ровняется 0,54смкорень из 48 Допустим дан треугольник АВС. Угол А = 90, Угол С = 60, а сторона Вс =8 см. Так как треугольник прямоугольный, угол А =90°, а угол С =60, то можно найти третий. Угол В= 180 - А- С = 180-90-60=30. Катет лежащии против угла 30° равен половине гипотенузы значит сторона АС=4см. По теореме Пифагора находим сторону АВ. АВ^2=ВС^-АС^2= корень квадратный 8-4 = корень квадратный из 4 =2. ПлощадьАВС равна половине произведения катетов. SАВС = (24):2 =4 Таким образом площадь равна 4 см Найдите площадь прямоугольного треугольника, если высота, проведённая к гипотенузе, делит ее на отрезки длинной 6см и 24см Есть правило: квадрат катета прямоугольного треугольника равен произведению гипотенузы и его проекции на гипотенузу: гипотенуза известна 24 + 6 = 30, проекции тоже известны: 24 и 6, значит один катет равен корень из (30/6)=корень из 5, а второй катет равен корень из (30/24)=корень из (1,25), а площадь прямоугольного треугольника: полупроизведение катетов: S= 1/2 корень из(51,25)=1/2 корень из (6,25)= 1/2 2,5=1,25 Ответ: 1,25 Решение на фотографии 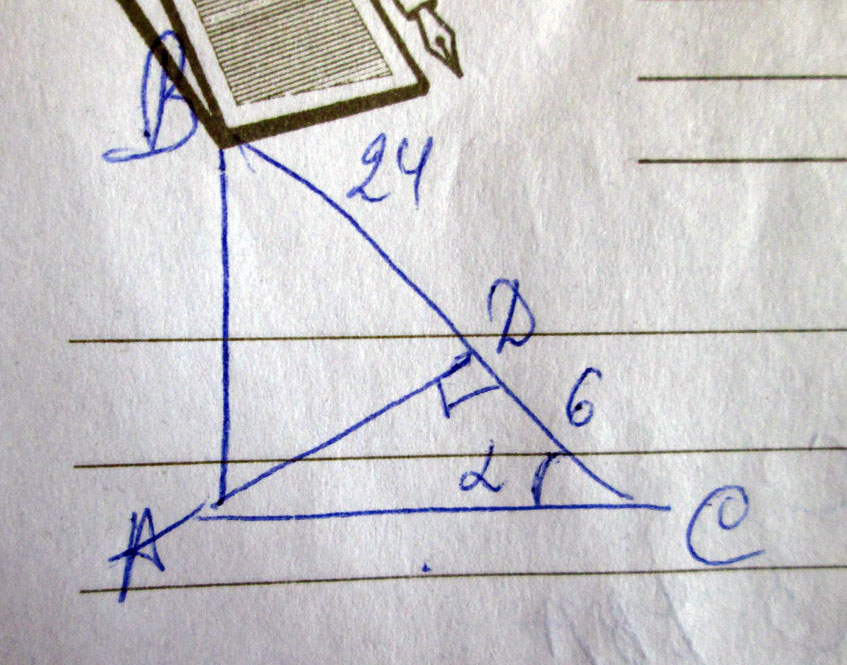Найдите площадь прямоугольного треугольника, если гипотенуза равна 4 а катеты равны, но не известны По т. Пифагора: С² = а ² + б²; Т. К. Катеты равны, то 2а² = с²; 2а²=16; А²=8; А= корень из 8; S = аа/2= 8/2=4; Ответ: 4. Пусть сторона треугольника = а. Тогда, по теореме Пифагора, гипотенуза^2 = сумма квадратов катетов. Значит 16=а^2+а^2 ( катетов равны по услов) 16=2а^2, отсюда а^2=8, а=корень из 8. S прямоуг треугольника равна 1/2произведение катетов. То есть S=1/2 корень из 8* корень из 8= 4 Найдите площадь прямоугольного треугольника, если гипотенуза 20 см, а сумма катетов - 28 см Примем длину одного из катетов за х (см), тогда длина второго равна 28 - х (см). Тогда по теореме Пифагора: 20² = (28 - х)² + х², то есть 400 = 784 - 56х + 2х², а значит, 2х² - 56х + 384. Поделим все уравнение на 2, тогда х² - 28х + 192. Т. К. Коэффициент b (при х) четный, то посчитаем D/4 = (b/2)² - ac = (-28/2)² - 192 = 14² - 192 = 196 - 192 = 4 = 2². Тогда х1 = ( -b/2 + √(D/4)) / a = ( - (-28/2) + √4 ) / 1 = 14 + 2 = 16 (см). А х2 = ( -b/2 - √(D/4) ) / a = ( - (-28/2) - √4 = 14 - 2 = 12. В первом случае длина 2го катета равна 28 - 16 = 12 см, тогда площадь равна их полупроизведению, а именно: S(прям. ∆) = ab/2, где а и b - длины катетов в одних и тех же единицах длины. Тогда S (прям. ∆) = ab/2 = 1612/2 = 166 = 96 см². При решении квадратного уравнения мы получили 2 корня, но, как мы видим, их сумма = 28, а значит, достаточно рассмотреть один из них и посчитать площадь. Может на всякий случай проверить: если же полученный х = 12, то длина второго катета равна 28 - 12 = 16 (см), а S(прям. ∆) = ab/2, где а и b - длины катетов в одних и тех же единицах длины. Тогда S(прям. ∆ ) = ab/2 = 1216/2 = 128 = 96 см². Ответ: S(прям. ∆) с катетами в 12 и 16 см равна 96 см². Найдите площадь прямоугольного треугольника, если его гипотенуза равна 12, а один из катетов - 5 Найдём второй катет по теореме Пифагора. Назовем АВ; АВ=корень квадратный из(144-25)=корень квадратный из 119. площадь равна половине произведения катетов==>S=5 корней из 119/2 По теореме Пифагора найдём второй катет 2катет(в квадрате)=гипотенуза(в квадрате) - 1 катет (в квадрате) 2 катет=(все под корнем) гипотенуза(в квадрате) - 1 катет (в квадрате) 2 катет=(все под корнем)144-25 2 катет =(все под корнем)119 Формула площади S=1/2ab Ult a и b катеты, ..........