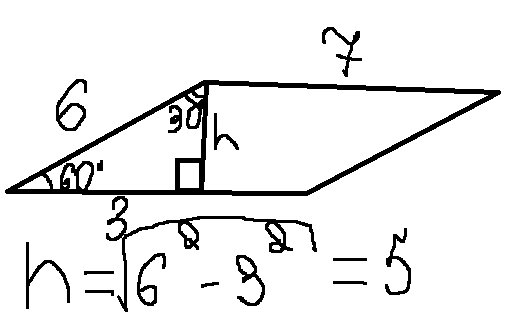Стороны параллелограмма равны 4 см.,угол между ними 45°. Найдите высоты параллелограмма


Главная Научный калькулятор
Меню Алгебра Геометрия Основные понятия Аксиомы планиметрии Углы Перпендикулярные и параллельные прямые Перпендикуляр и наклонная Круг (окружность) Треугольник Четырехугольник Параллелограмм Трапеция Многоугольники Основные понятия стереометрии Аксиомы стереометрии Прямые в пространстве Пересекающиеся прямые Параллельные прямые Скрещивающиеся прямые Прямая и плоскость в пространстве Перпендикулярность прямой и плоскости Параллельность прямой и плоскости Угол между прямой и плоскостью Теорема о трех перпендикулярах Формула двойного проектирования Плоскости в пространстве Пересекающиеся плоскости Параллельность плоскостей Перпендикулярность плоскостей Площадь проекции плоской фигуры на плоскость Многогранники: Пирамида Призма Тела вращения: Цилиндр Конус Шар (Сфера) Объем тел вращения Задачи по геометрии Примеры решений Вспомогательные материалы: Таблицы Брадиса Исследование функций Асимптоты. Первая производная. Вторая производная. Тригонометрия Тригонометрические неравенства Преобразования графиков	Треугольник : Равнобедренный треугольник : Прямоугольный треугольник : Четырехугольник : Параллелограмм : Ромб : Прямоугольник : Трапеция : Многоугольники : Круг и окружность : Прямые и плоскости : Пирамида : Пространственная система координат : Цилиндр : Конус : Углы : Призма : Параллелепипед : Сфера и Шар Стороны параллелограмма равны 4 см. , угол между ними 45°. 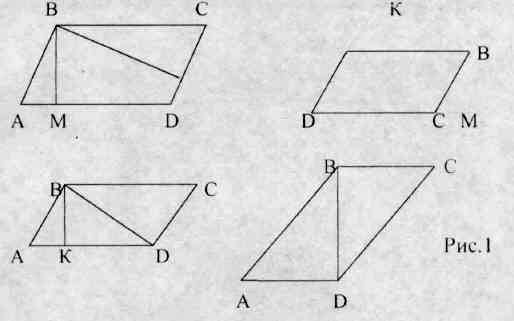Найдите высоты параллелограмма Решение: Высота будет равна 4sin45=4(√2)/2=2√2 Опускаем перпендикуляр BH к AD.Рассмотрим треугольник АВН. В нем: угол АНВ=90, угол ВАН=45, угол АВН=180-(90+45)=45. соsВ=ВН/АВ; √2/2=ВН/4; ВН=(4√2)/2=2√2 первый рисунок Рассмотрим треугольник АВМ угол а 45 гр. угол ВМА 90гр. Отсюда угол АВМ=180-90-45=45 Треугольник АВМ равнобедренный АМ=ВМ 16=АМ^2+ВМ^2 АМ=ВМ=корень из 8= 2 корень из 2 Стороны параллелограмма равны 4см и 5см, угол между ними 45°. Найдите высоты параллелограмма. Площадь параллелограмма равна произведению его сторон на синус угла между ними Площадь параллелограмма равна произведению его стороны на высоту проведенную к ней Отсюда: Площадь параллелограмма равна S=ab sin A S=45sin 45=20корень(2)/2=10корень(2) кв. см Высота, проведенная к стороне длиной 4 см, равна h(a)=S/a h(a)=10корень(2)/ 4=*2.5 корень(2) см** Высота, проведенная к стороне длиной 5 см, равна h(b)=S/b h(b)=10корень(2)/5=2корень(2) см Стороны параллелограмма равны 6 и 7 см, угол между ними 60°. Найдите высоты параллелограмма. Отметим параллелограмм как АВСД Опустим перпендикуляр из вершины В на основание АД. Угол между сторонами 60°. Значит верхний угол прямоугольного треугольника равен 30°. Так сторона, лежащая напротив угла в 30 гр. равна половине гипотенузы, значит нижний катет равен 3. Тогда, по теореме Пифагора найдем: H1 = √(36-9) = √27 = 3√3 = H1 Вторую высоту найдем через площадь, так легче: S = 3√3 * 7 = 21√3 S = h26 = 21√3, h2 = 21√3/6 = 3,5√3* В параллелограмме высоты будут равные. Найдем одну из них, используя метод площадей: S=ah.S=absina. (a и b - стороны. Синус альфа - синус угла между этими сторонами, h - высота). Приравняв два метода нахождения площади, получим, что h=2 корень из 2 Сторону АС найдем через определение тангенса угла альфа. Т.е. tga=CB/AC.AC=CB/tga=5/tga Используем основное тождество, чтобы найти косинус (через него найдем тангенс).\( cos^{2}a=1- sin^{2}a \) \( cosa= \sqrt{ \frac{144}{169} } = \frac{12}{13} \) \( tga= \frac{sin}{cos} \) \( tg=5/13 13/12=5/12 \) Cтавим высоту на рисунке, обозначаем углы в треугольнике; против угла в 30° лежит катет, равный половине гипотенузы, а потом по Пифагору В прямоугольном треугольнике 180 - 60 = 30, а сторона лежащая напротив угла в 30° равна половине гипотенузы, зн 6/2=3, а потом по Пифагору 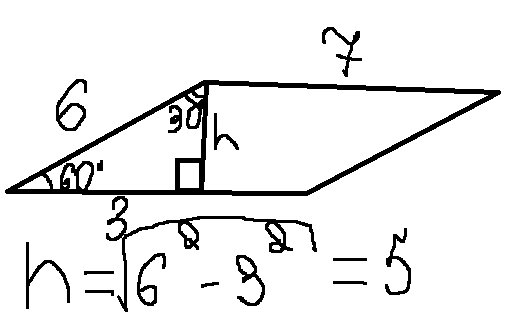Стороны параллелограмма равны 6см и 7см, угол между ними равен 55°. Найдите высоты параллелограмма и его площадь Площадь параллелограмма = произведению сторон на синус угла между ними S = ab sin α, S = 67sin 55° = 34 cм2. С другой стороны площадь равна произведению стороны на высоту. Тогда одна высота h1 = S/a = 34/6 =5,7 (см), а другая высота h2 = S/b = 34/7 = 4,9(см) Ответ: 34см2, 5,7см, 4,9см допустим 7-основание,6-бок сторона, хотя это не принципиально, тогда H1=6sin(55)=60.82=4.92(см) H2=7sin(55)=5.74(см) S=7H1=74.92=34.44(смкв) 1. В параллелограмме ABCD AD=12см, AB=6см, уголBAD=60°. Биссектриса угла D пересекает BC в точке Е. 1)найдите высоты параллелограмма и его площадь. 2)определите вид треугольника ECD и найдите длину описанной около тругольника окружности. 3) найдите длину большей диагонали параллелограмма. В параллелограмме ABCD AD=12см, AB=6см, уголBAD=60°. 1 площадь S=ABADsin60=125√3/2 =30√3 см2 площадь S=ABh1 ; h1 = S/AB = 30√3 / 6= 5√3 <-высота 1 площадь S=ADh2 ; h2 = S/AD = 30√3 / 12= 2,5√3 <-высота 2* 2 угол <BAD=60° угоп <D = 180 - <BAD = 180 - 60 =120 град <D / 2 = 120 /2=60 <C =<BAD=60° Биссектриса угла D пересекает BC в точке Е. треугольник ECD -равносторонний, так как все углы 60 град стороны треугольника ECD тоже равны b =DE=EC=CD=AB= 6 см радиус описанной окружности R = b√3/3 =6√3/3=2√3 см длина окружности L=2Rп=22√3п=4п√3 см <-обычно в таком виде 3 длина большей диагонали параллелограмма. По теореме косинусов d^2 = AB^2+AD^2 - 2ABADcos <D d^2 = 6^2 +12^2 -2612 cos120 =252 d = √252 = 6√7 <-длина большей диагонали Стороны параллелограмма равны 24 см,25 см. Малая диагональ параллелограмма равна 7см. Найдите высоты параллелограмма. Параллелограмм АВСД, АВ=24, АД=25, ВД=7 cosA=(АВ в квадрате + АД в квадрате - ВД в квадрате) / 2 х АВ х АД cosA = (576+625-49) / 2 х 24 х 25 cosA =0,96 sinA = корень(1 - cosA в квадрате) = 0,28 площадь параллелограмма = АВ х АД х sinA = 24 х 25 х0,28 =168 высота1 = 168/24 =7 высота2 = 168/25 = 6,72 треугольник АВД - прямоугольный, АД -гипотенуза = сумме квадратов АВ и ВД ВД - высота - перпендикулярно АВ 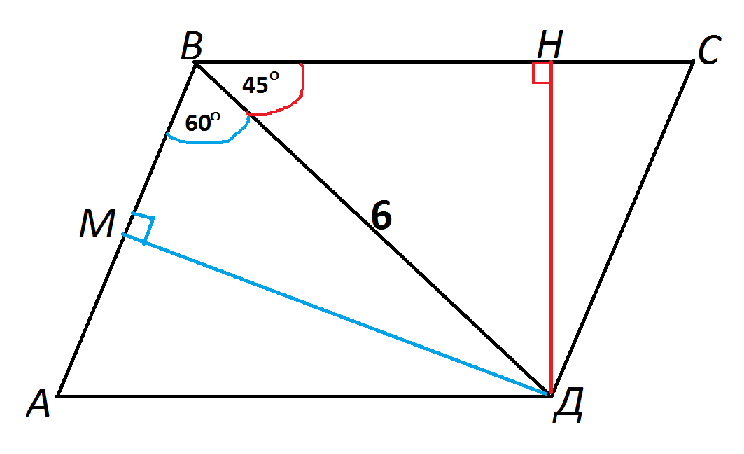В параллелограмме одна из диагоналей равна 6 см и образует со сторонами параллелограмма углы 45 и 60°. Найдите высоты параллелограмма. Пусть дан параллелограмм АВСД. Тупой угол при вершине В параллелограмма равен 60°+45°. То есть Угол АВД=60°, угол СВД=45° Проведем высоту ДН из угла Д к ВС. Она образует прямоугольный равнобедренный треугольник с катетами ВН и ДН и гипотенузой ВД. ДН=ВДsin 45°=6√2):2=3√2 см Высота ДМ из Д к АВ образует с диагональю ВД прямоугольный треугольник ДМВ с острым углом МВД= 60° и гипотенузой ВД=6 см ДМ=ВДsin 60°=6√3):2=3√3 см Ответ: Высоты равны 3√2 см и 3√3 см.