Высота правильной треугольной призмы ABCA1B1C1 равна 2 см, а сторона AB


Главная Научный калькулятор
Меню Алгебра Геометрия Основные понятия Аксиомы планиметрии Углы Перпендикулярные и параллельные прямые Перпендикуляр и наклонная Круг (окружность) Треугольник Четырехугольник Параллелограмм Трапеция Многоугольники Основные понятия стереометрии Аксиомы стереометрии Прямые в пространстве Пересекающиеся прямые Параллельные прямые Скрещивающиеся прямые Прямая и плоскость в пространстве Перпендикулярность прямой и плоскости Параллельность прямой и плоскости Угол между прямой и плоскостью Теорема о трех перпендикулярах Формула двойного проектирования Плоскости в пространстве Пересекающиеся плоскости Параллельность плоскостей Перпендикулярность плоскостей Площадь проекции плоской фигуры на плоскость Многогранники: Пирамида Призма Тела вращения: Цилиндр Конус Шар (Сфера) Объем тел вращения Задачи по геометрии Примеры решений Вспомогательные материалы: Таблицы Брадиса Исследование функций Асимптоты. Первая производная. Вторая производная. 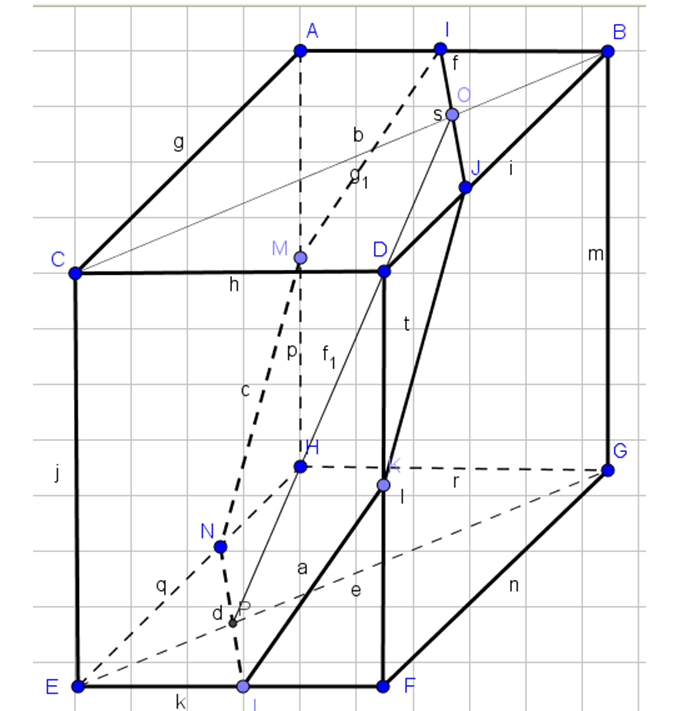Графики функций Задачи по функциям Тригонометрия Тригонометрические неравенства	Треугольник : Равнобедренный треугольник : Прямоугольный треугольник : Четырехугольник : Параллелограмм : Ромб : Прямоугольник : Трапеция : Многоугольники : Круг и окружность : Прямые и плоскости : Пирамида : Системы координат : Цилиндр : Конус : Углы : Призма : Параллелепипед : Сфера и Шар : Построения Высота правильной треугольной призмы ABCA1B1C1 равна 2 см, а сторона AB равна 4 см. Чему будет равна площадь сечения этой призмы плоскостью, проходящей через точки A, B1, C? Решение: Полученное сечение - это треугольник, т.к. призма правильная, то стороны основания а именно: АС, СВ, АВ равны. Также равны и ребра : АА₁, СС₁, ВВ₁ равны, из треугольников АВ₁В находи сторону АВ по теореме Пифагора из треугольника СВ₁В находим СВ₁ тоже по теореме Пифагора. Как найдём все стороны этого сечения по теореме Герона находим площадь. 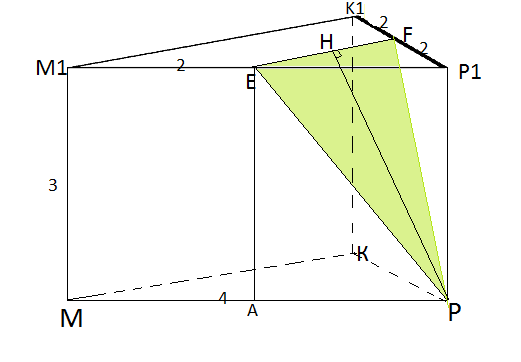Вот теорема Герона S=корень квадратный из полупериметра треугольника умножить на (полупериметр минус первая сторона ) умножить на полупериметр минус вторая сторона) и умножить на (полупериметр минус третья сторона) MKPM₁K₁P₁ — правильная треугольная призма, сторона основания которой 4 см. Найдите площадь сечения призмы плоскостью, проходящей через точки Р, Е и F, где Е и F — середины ребер M₁P₁ и К₁Р₁, а боковое ребро равно 3 см. Площадь пересечения плоскости с призмой равна площади треугольника ЕFP. Площадь ΔЕFP = ½PHEF Найдем значение EF. ΔЕР₁F подобен Δ M₁K₁P₁. Все стороны ΔM₁K₁P₁ равны 4. При этом ЕР₁=½М₁Р₁=2 см. ⇒ все стороны ΔЕР₁F равны 2 : FP₁=EP₁=EF=2 см EF=2* Найдем значение PH. Из ΔЕАР выразим значение EP: EP²=EA²+AP² Так как боковое ребро правильной призмы равно 3, то ЕА=ММ₁=3 см АР=МР/2 = 2, где МР=4 см - сторона основания призмы. EP²=9+4=13 см² Из ΔЕРН выразим РН: РН²=ЕР²-ЕН²=13-1=12 см² PH=2√3 см Посчитаем площадь ΔЕРF: S ΔEPF = ½PHEF= ½ 2√3 * 2= 2√3 см² Ответ. Площадь пересечения призмы с плоскостью EFP равна 2√3 см² В основании прямой призмы параллелограмм со сторонами 4 дм и 5 дм и углом между ними 30°. Найдите площадь сечения призмы плоскостью, если известно, что она пересекает все боковые ребра и образует с плоскостью основания угол 45°. Основание является ортогональной проекцией сечения на плоскость (на плоскость, в которой это основание лежит). Поэтому площади сечения Sc и основания S связаны так Sccos(Ф) = S; Ф - заданный в задаче угол в 45°. Осталось найти площадь основания, что совсем просто S = absin(A); где А - угол между сторонами основания. Он тоже задан - 30°. Собираем все, и получаем Sc = 45(1/2)/(корень(2)/2) = 10корень(2) В прямой призме ABCA₁B₁C₁ AC=13 AB=14 BC=15 AA₁=10. Точки М и Н – середины ребер АА1 и ВВ1 соответственно. Найдите площадь полной поверхность призмы Найдите площадь сечения призмы плоскостью MHC 3)Найдите угол между плоскостями MHC и ABC 4) Найдите угол между прямой АА₁ и плоскость MHC 5)Разложите вектор МК по векторам АА₁, АС и АВ, если К-середина СН 6)Постройте линию пересечения плоскостей МНС и АВС 1.S=abc=101415=2100 2. Sсеч. =Sпрям-ка=MDMH=ab. MD=(5 в квадрате+15 в квадрате)-все это из под корня (теорема Пифагора)=корень квадратный из 250. Sсеч. =Sпрям-ка=корень квадратный из 25014=14квадратный корень из 250 3. Угол между плоскостями=угол BCH=по теореме косинуса. 4. 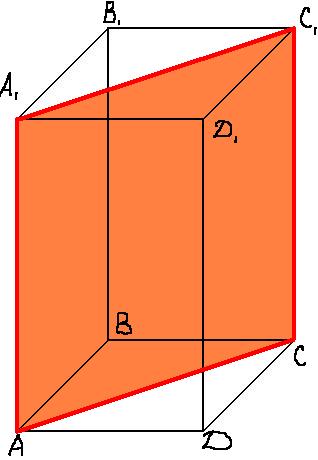Угол этот будет равен-180-90-(получившегося углу из 3 задания) В правильной четырехугольной призме ABCDA₁B₁C₁D₁ ребро АА₁=15, а диагональ BD₁ = 17. Найдите площадь сечения призмы плоскостью, проходящей через точки А, А₁, С. Построение: 1) Соединим точки А и А₁, так как они лежат в одной плоскости. 2) Соединим точки А и С, так как они лежат в одной плоскости. 3) Так как основания призмы параллельны друг другу, а плоскость (в данном случае сечения) пересекает параллельные плоскости по параллельным прямым, то проведем А₁С₁\|\|АС. 4) Соединим точки С1 и С, так как они лежат в одной плоскости. 5) Получим искомое сечение АА₁С₁С. Решение: \( S_{AA_1C_1C}=AA_1\cdot AC=AA_1\cdot BD \\\ BD_1^2=BD^2+DD_1^2=BD^2+AA_1^2 \\\ BD= \sqrt{BD_1^2-AA_1^2} \\\ S_{AA_1C_1C}=AA_1\sqrt{BD_1^2-AA_1^2} \\\ S_{AA_1C_1C}=15\cdot \sqrt{17^2-15^2} =120 \) *Ответ: 120* В прямой призме ABCA₁B₁C₁ угол ABC=90°, угол CAB =60°, AB=2 см, AA₁= 2 корень из 3. 1) Найдите площадь полной поверхности прямой призмы 2) Найдите площадь сечения призмы плоскостью A₁BC 3) Найдите угол между плоскостями A₁BC и ABC 4) Найдите угол между прямой CC₁ и плоскостью A₁BC. 5) Докажите, что плоскость A₁BC перпендикулярна плоскости AA₁B₁ В ΔАВС: АС=22=4(см)(гипотенуза=удвоенному катету, лежащему напротив угла 30°) ВС²=АС²-АВ² ⇒ВС=√4²-2²=2√3(см). Sосн=1/2АВСВ=1/222√3=2√3(см²). Sбок=РН=(2+4+2√3)2√3=12√3+12=12(√3 +1)(см²). 1) Sполн=2Sосн+Sбок=22√3+12(√3 +1)=4√3+12√3+12=16√3+12(см²). 2) ПлоскостьА₁ВВ-тр-к, уголА₁ВС=90°(теорема о трех перпендикулярах) SΔ=1/2А₁ВВС; из ΔА₁АВ найдем ВС: ВС²=АА₁²+АВ²; ВС=√(2√3)²+2²=√12+4=√16=4(см). SΔА₁ВС=1/242√3=4√3(см²). 3) Двугранный угол между плоскостями А₁ВС и АВС лежит в плоскости, перпендикулярной ВС. (плоскость АА₁В₁В) это угол А₁ВА = α tgα=2√3/2=√3 ⇒ α = 60°. 4) СС₁ параллельна ВВ₁. Угол между прямой и плоскостью ищем в плоскости АА₁ВВ₁, перпендикулярной плоскости А₁ВС. Это угол А₁ВВ₁. Угол А₁ВВ₁ = 90-α = 90-60 = 30°. 5) АВ₁ лежит в плоскости, перпендикулярной А₁ВС (по теореме о трех перпендикулярах), значит, и плоскость перпендикулярна А₁ВС. В правильной треугольной призме ABCA₁B₁C₁ AB=2 см, AA₁=1 см. 1) Найдите площадь полной поверхности призмы. 2) Найдите площадь сечения призмы плоскостью ACB₁. 3) Найдите угол, который составляет прямая AB₁ с плоскостью ABC. 4) Найдите угол между плоскостями AB₁C и ABC. 5) Найдите длину вектора AA₁-AC+2B₁B-C₁C 6) Докажите, что прямая A₁C₁ параллельна плоскости ACB₁. 1) В основании правильной треугольной призмы лежит правильный треугольник со стороной АВ = 2. По свойствам правильного треугольника Sосн. = √3⋅АВ^2/ 4 Таких оснований у нас 2. Сторона призмы это прямоугольник со сторонами АВ = 2 и АА1 = 1 S бок = АВ АА1, Таких сторон у нас 3. Получаем Sполное = 2Sосн. + 3 Sбок. = 2 * √3⋅АВ^2/ 4 + 3 АВ АА1 = 2√3⋅2^2/4 + 3 21 = 2√3 +6 = 9,46 см2 2) треугольник АСВ1 равнобедренный Основание АС =2 см, Надо найти ВН - высота, в равнобедренной треугольнике она является медианой и биссектрисой Из прямоугольника СС1ВВ1 найдем СВ1 СВ = 2 см, ВВ1 = 1 см СВ1^2 = CB^2+BB1^2 CB1^2 = 2^2 +1^2 = 5 CB1 = корень из 5 Треугольник НВ1С прямоугольный, В1Н^2 = CB1^2 - HC^2 HC = AC /2 = 2/2 = 1см B1H^2 = (корень из 5)^2 - 1^2 = 5-1 = 4 B1H = 2 cм S = B1HAC /2 S = 2 2 /2 = 2 cm^2 3) рассмотрим треугольник АВВ1 - он прямоугольный т.к. Призма правильная надо найти угол ВАВ1 tg BAB1 = BB1/ AB = 1/2 примерно 27° 4) т.к. Прямая АВ1 принадлежит плоскости АВ1С, значит этот угол есть то, что мы искали в п. 3 дальше подумаю. В правильной треугольной призме ABCA1B1C1 AB=2 см, AA1=1 см. 1) Найдите площадь полной поверхности призмы. площадь основания S1 =ABABsin(pi/3)1/2 = корень(3) боковая площадь S2 =ABAA13 = 213=6 площадь полной поверхности призмы S3 = 2S1+S2 = 2корень(3) + 6 2) Найдите площадь сечения призмы плоскостью ACB1. площадь основания S1 = ABABsin(pi/3)1/2 = корень(3) высота треугольника основания h =ABsin(pi/3)=корень(3) высота треугольника сечения h1 = корень(h^2+AA1^2)=2 площадь сечения призмы плоскостью ACB1 S4 = S1h1/h = корень(3) 2/корень(3) = 2 3) Найдите угол, который составляет прямая AB1 с плоскостью ABC. тангенс угла = BB1/AB=1/2 угол = арктангенс(0,5) 4) Найдите угол между плоскостями AB1C и ABC. высота треугольника основания h =ABsin(pi/3)=корень(3) тангенс угла = BB1/h=1/корень(3) угол = арктангенс(1/корень(3)) = pi/6 = 30° 5) Найдите длину вектора AA1-AC+2B1B-C1C AA1-AC+2B1B-C1C=CА+B1B+СC1=CА+A1A+AA1=CA ответ - 2 см 6) Докажите, что прямая A1C1 параллельна плоскости ACB1. прямая A1C1 параллельна прямой АС, лежащей вплоскости ACB1, значит параллельна плоскости ACB1 Ребра AB=BC=BB₁ треугольной призмы ABCA₁B₁C₁ попарно перпендикулярны, и равны 4 корня из 2 (4\( \sqrt{2} \)). Найдите площадь сечения призмы плоскостью, походящей через середины ребер AB, AA1, BC В сечении образуется равнобокая трапеция. Обозначим середины сторон АВ и ВС точками К и М. Отрезок КМ параллелен (как средняя линия треугольника) гипотенузе АС и равен её половине. АС = АВ√2 = 4√2 * √2 = 8. КМ = (1/2)8 = 4. Боковые грани призмы пересекаются по отрезкам ДК и ЕМ. Так как КМ параллелен АС, то линия пересечения заданной плоскостью грани АА₁С₁С линия ДЕ параллельна АС. Боковая сторона полученной трапеции равна: ((4√2)/2) √2 = 4. Высота трапеции равна √(4²-((8-4)/2)²) = √(16-4) = √12= =2√3. Площадь сечения призмы плоскостью, проходящей через середины ребер AB, AA1; BC, имеющего форму трапеции, равна 2√3 * ((8+4)/2) = 12√3. Дана правильная треугольная призма ABCA₁B₁C₁, сторона основания которой равна 6. Найдите площадь сечения призмы плоскостью, проходящей через сторону AB под углом 30° к основанию. Пусть середина A1C1 = K сечения=AB, вторая=AKиз точки K должна пойти прямая \|\| AB => \|\| и A1B1, т.е. Получим отрезок KD (D лежит на B1C1), KD \|\| A1B1 и проходит через середину A1C1 => KD - средняя линия треугольника A1B1C1KD = 1/2 * A1B1 = 1/2 * AB = 1/2 * 6 = 3и четвертая сторона сечения BD получился четырехугольник AKDB, в кот. AB\|\|DK => AKDB - трапеция. S трапеции = 1/2 * (BA+DK) * KF (KF - высота трапеции)из треуг. AA1K по т. Пифагора AK = корень(AA1^2 + A1K^2) = корень(44 + 33) = корень(16+9) = корень(25) = 5 (AA1 = 4 - боковое ребро, A1K = 1/2 * A1C1 = 1/2 * 6 = 3)AK - боковая сторона трапеции (сечения), трапеция равносторонняя => в треугольнике AFK FA = (AB-DK)/2 = (6-3)/2 = 3/2 => высота трапеции из прямоугольного треуг. AFK по т. Пифагора FK = корень(AK^2 - FA^2) = корень(55 - 9/4) = корень(25 - 9/4) = корень(91/4) = корень(91)/2S = 1/2 (6 + 3) * корень(91)/2 = 9корень(91)/4Надеюсь, нигде не ошиблась. Равносторонняя => в треугольнике AFK FA = (AB-DK)/2 = (6-3)/2 = 3/2 => высота трапеции из прямоугольного треуг. AFK по т. Пифагора FK = корень(AK^2 - FA^2) = корень(55 - 9/4) = корень(25 - 9/4) = корень(91/4) = корень(91)/2S = 1/2 * (6 + 3) * корень(91)/2 = 9корень(91)/4 В правильной четырёхугольной призме ABCDA1B1C1D1 ребро AA1 = 8, а диагональ BD1 = 17. Найдите площадь сечения призмы плоскостью, проходящей через точки A, A1 и C. Плоскость сечения будет проходить через вершины А, А1, С и С1 т.к. АА1\|\|СС1 и АС\|\|А1С1. В правильной четырёхугольной призме диагонали ВД1 и АС1 равны. Поскольку в основании квадрат, то АС=ВД; все боковые рёбра призмы равны, значит в прямоугольных треугольниках АСС1 и ВДД1 катеты равны, следовательно равны и гипотенузы АС1 и ВД1. В тр-ке АСС1 АС²=АС1²-СС1²=17²-8²=225, АС=15. АСС1А1 - прямоугольник, площадь которого: S=АС·АА1=15·8=120 (ед²) В правильной шестиугольной призме A B C D E F A1 B1 C1 D1 E1 F1 Стороны основания равны 5 А боковые ребра равны 11 Найдите площадь сечения призмы плоскостью проходящей через вершины C, A1 F1 В сечении - шестиугольник, две стороны "а" которого F1А1 и ДС являются рёбрами призмы длиной по 5. 4 остальные стороны - следы сечения боковых граней призмы. Они равны √(5²+(11/2)²) = √(25+30,25) = √55,25. Высота шестиугольника равна √(АС²+СС1²) = √((2acos30°)²+11²) = = √((25(√3/2))² + 121) = √(75+121) = √196 = 14. Площадь шестиугольника S равна сумме площадей прямоугольника S1 и двух треугольников, площадь S2 которых можно найти по формуле Герона. S1 = 514 = 70. S2 = 2√(p(p-a)(p-b)(p-c), где р - полупериметр, равный (а+в+с)/2 = = (14+2√55,25)/2 = 7+√55,25 ≈ 14,43303. Тогда S2 = 217,5 = 35. Ответ: S = 70 + 35 = 105. В правильной четырехугольной призме MNPQM1N1P1Q1, сторона основания равна 11, а боковое ребро 15. На рёбрах M1Q1,M1N1 и PQ взяты точки X,Y,Z, соответственно так, что Q1X=N1Y=QZ=5. Найдите площадь сечения призмы плоскостью XYZ В сечении получим шестиугольник с попарно параллельными сторонами, имеющий симметрию относительно диагональной плоскости призмы. Верхнее и нижнее основания его равны (11-5)√2 = 6√2. Высота L его лежит в диагональной плоскости призмы и равна: L = √(15²+(5√2)²) = √(225+50) = √275 = 5√11. Площадь можно разделить на прямоугольник и 2 равных равнобедренных треугольника. S = (6√2)(5√11)+2(1/2)(2,5√2)*(5√11) = 42,5√22 ≈ 199,3427 кв. ед.