Высота конуса H. Образующая l, найти R

Решение:
Если нарисовать это то получитcя что образующая конуса, высота и радиус это все вместе будет прямоугольный треугольник,где образующая конуса l это гипотенуза а Н и R это катеты.тогда по теореме Пифагора найдем R(радиус).так как это один из катетов то его квадрат равен квадрат гипотенузы - квадрат высоты (R^2=l^2-H^2).а сам радиус равен корень из полученного числа.то есть все можно представить формулой R=sqrt(l^2-H^2).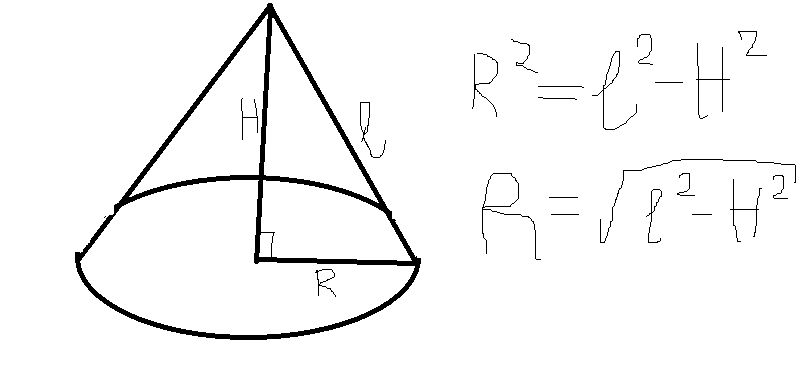

Высота конуса 3 см, а образующая 5 см. Найти радиус конуса и длину окружности основания.

h=3 см
l=5 cм

по теореме Пифагора r=корень(l^2-h^2)=корень(5^2-3^2)=4 см
длина окружности равна c=2*pi*r=2*pi*4= 8*pi cм (или 8*3.14=25.12 см)

Если высота равна 3, а образующая 5, то получается прямоугольный треугольник, где образующая - гипотенуза. По теореме Пифагора, \( r^2=5^2 - 3^2 \), отсюда r=4. 
Длина окружности \( 2\pi R \) то есть \( 2\pi \cdot 4=8\pi \)

Образующая конуса равна 10, высота конуса 6, найти радиус конуса

Конус АВС, АВ = ВС = 10, ВО - высота = 6, треугольник АВО прямоугольный, АО - радиус = корень(АВ в квадрате - ВО в квадрате) = корень(100-36)= 8

Высота конуса равна 8 см, угол при вершине осевого сечения равен 60°. Найти радиус конуса и площадь его осевого сечения.

\( S = R*H \)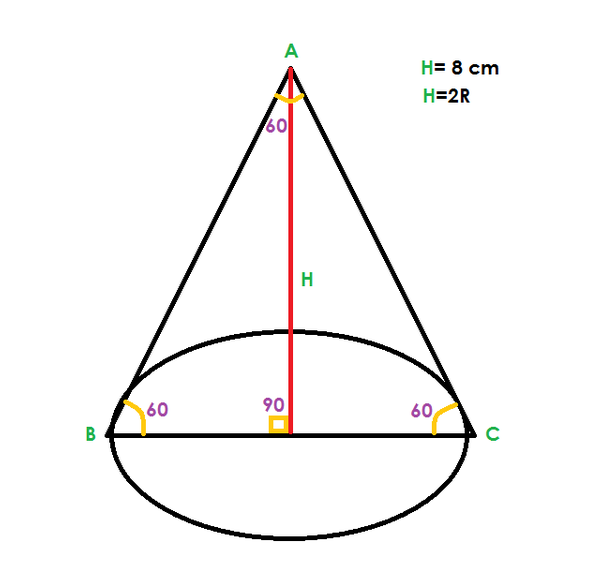
{Если угол при вершине равен 60°, то осевым сечением конуса будет равносторонний треугольник. Его сторона равна образующей, то есть 8 см.  Тогда радиус основания равен половине стороны и равен 4 см. }
\( 2R=H \)
\( R= H/2 \)
\( R=4 \)
\( S = 4*8 \)
Досчитайте сами, ответ записывается в \( cm^{2} \).

Найдите радиус конуса, если известна образующая конуса = 10, и угол образующей с осью = 30°

Образующая является гипотенузой прямоугольного треугольника с катетами, являющимися радиусом и высотой. Радиус лежит против угла в 30гр⇒R=1/2L=1/2*10=5

Образующая, ось конуса и радиус конуса образут прямоугольный треугольник
cosa=R/L
R=L*cos60=10*0,5=5
Ответ R=5 cм

Перпендикуляр, проведенный из центра основания конуса на образующую, делит их на отрезки 36 см и 64 см (считая от вершины конуса). Найти радиус основания конуса

Перпендикуляр делит треугольник ABO на 2 треугольника BOH и OAH. Все 3 треугольника подобны друг другу, поэтому можно составить пропорции:AH / OH = OH / BH36 / OH = OH / 64OH ^ 2 =36 * 64OH = корень (36 * 64) = 6 * 8 = 48воспользовавшись теоремой Пифагора для треугольника BOH найдём гипотенузу:BO = корень(OH ^ 2 + BH ^ 2) = корень (48 ^ 2 + 64 ^ 2)= корень (16*16 * 3*3 + 16*16 * 4*4) = = 16 * корень(25) = 16*5 = 80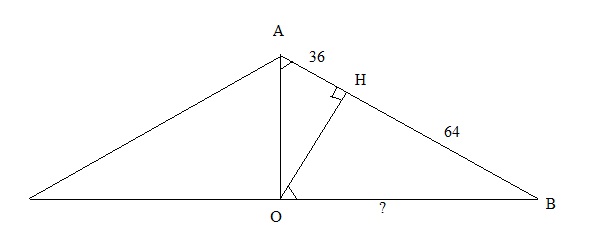

Объем конуса равен 75π, высота равна 9. Найти радиус основания конуса

По формуле объёма конуса
\( V= \frac{1}{3}\pi*r^2*h \)
Здесь r - искомый радиус,
h - высота, h=9,
V - объём конуса, V=75π.
Подставим известные данные в вышеуказанную формулу
\( 75\pi= \frac{1}{3}\pi*r^2*9 \)
75π=3π*r²   Делим обе части на 3π.
25=r²
r=5  - так как отрицательный ответ не подходит по смыслу задачи.
Ответ: радиус конуса равен 5.

Высота конуса = 4 см. А образующая = 5 см. Найдите радиус основания конуса.

Образующая-ВС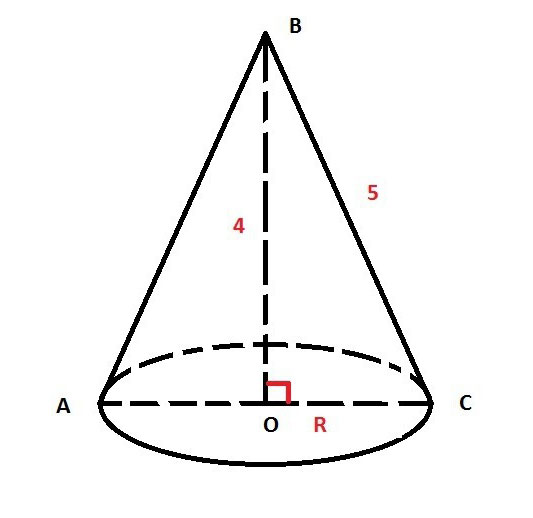
высота-ВО
R=ОС-радиус
Находим радиус из прямоугольного треугольника ОВС
R=√(BC²-BO²)=√(5²-4²)=3
Ответ: 3