Диагонали прямоугольника ABCD пересекаются в точке О, угол ABO=36°. Найдите угол AOD


Главная Научный калькулятор
Меню Алгебра Геометрия Основные понятия Аксиомы планиметрии Углы Перпендикулярные и параллельные прямые Перпендикуляр и наклонная Круг (окружность) Треугольник Четырехугольник Параллелограмм Трапеция Многоугольники Основные понятия стереометрии Аксиомы стереометрии Прямые в пространстве Пересекающиеся прямые Параллельные прямые Скрещивающиеся прямые Прямая и плоскость в пространстве Перпендикулярность прямой и плоскости Параллельность прямой и плоскости Угол между прямой и плоскостью Теорема о трех перпендикулярах Формула двойного проектирования Плоскости в пространстве Пересекающиеся плоскости Параллельность плоскостей Перпендикулярность плоскостей Площадь проекции плоской фигуры на плоскость Многогранники: Пирамида Призма Тела вращения: Цилиндр Конус Шар (Сфера) Объем тел вращения Задачи по геометрии Примеры решений Вспомогательные материалы: Таблицы Брадиса Исследование функций Асимптоты. Первая производная. Вторая производная. Тригонометрия Тригонометрические неравенства Преобразования графиков	Треугольник : Равнобедренный треугольник : Прямоугольный треугольник : Четырехугольник : Параллелограмм : Ромб : Прямоугольник : Трапеция : Многоугольники : Круг и окружность : Прямые и плоскости : Пирамида : Пространственная система координат : Цилиндр : Конус : Углы : Призма : Параллелепипед : Сфера и Шар Диагонали прямоугольника ABCD пересекаются в точке О, угол ABO=36°. Найдите угол AOD Решение: 1) треугольник ABD-прямоугольный, т.к. угол А равен 90°, значит угол BDA = 90-36 = 54, как сумма острых углов прямоугольного треугольника 2) треугольник ABD равен треугольнику ACD по двум катетам или по катету и гипотенузе, отсюда следует, что угол BDA равен углу CAD = 54 3) Рассмотрим треугольник AOD: угол CAD = углу BDA =54 а угол AOD = 180 - 54 - 54 = 72 (как сумма углов в треугольнике) Ответ 72 1. Диагонали прямоугольника равны (свойство прямоугольника) АС = BD 2. Диагонали прямоугольника точкой пересечения делятся пополам (свойство параллелограмма) AO=BO=CO=DO Значит, треугольника АОВ - равнобедренный с равными боковыми сторонами АО и ВО. 3. Углы при основании равнобедренного треугольника равны (свойство равнобедренного треугольника): угол АВО = углу ВАО 4. Угол AOD - внешний угол треугольника АОВ. Градусная мера внешнего угла треугольника равна сумме двух внутренних углов этого треугольника, не смежных с ним: ∠AOD = ∠ABO + ∠BAO = 36° + 36° = 72° Так как диагонали точкой пересечения делятся пополам, то они образуют 4 равнобедренных треугольника. Треугольник АВО равнобедренный (ВО=ОА), соответственно угол АВО равен углу ОАВ=36° Сумма углов треугольника = 180, поэтому угол ВОА = 180-36-36=108° АОD смежный угол с углом ВОА, а так как они в сумме образуют 180° То ВОА=180-108=72° Угол АВО находится в треугольнике АОВ, который является равнобедренным (свойства прямоугольника). угол ВАО = углу АВО = 36. Так как все углы треугольника дают в сумме 180°, то угол ВОА = 180 - 36 - 36 = 108. Углы ВОА и АОД - смежный. Сумма смежных углов равна 180°, и, чтобы найти АОД, нужно от 180 отнять 108 и это равно 72. Ответ 72. Сначала найдём угол AOB. Треугольник AOB - равнобедренный с основанием AB, углы ABO и BAO равны 36°. Угол AOB равен 180 - 2 * 36 = 108°. Угол AOD равен 180 - AOB = 180 - 108 = 72°. Имеем прямоугольник ABCD. Диагонали AC и BD, которые пересекаются в точке O. Угол ABO=36°. Найти угол AOD. Т. К. диагонали прямоугольника равны и точкой пересечения делятся пополам, то треугольник ABO - равнобедренный. Значит, ABO=BAO=36.ABO+BAO+AOB=180°. Угол AOB= 180-(ABO+BAO). угол AOB=180 - (36+36)=108. Т.к. AOB+AOD=180 (эти углы смежные), то AOD=180-108=72°. Имеем прямоугольник ABCD. Диагонали AC и BD, которые пересекаются в точке O. Угол ABO=36°. Найти угол AOD. Т. К. диагонали прямоугольника равны и точкой пересечения делятся пополам, то треугольник ABO - равнобедренный. Значит, ABO=BAO=36.ABO+BAO+AOB=180°. Угол AOB= 180-( ABO+BAO). угол AOB=180 - (36+36)=108. Т.к. AOB+AOD=180(эти углы смежные), то AOD=180-108=72°. Диагонали прямоугольника ABCD пересекаются в точке О. Найдите угол AOD, если углы относятся CBD:ABD=2:3. Ответ дайте в градусах. Пусть угол СВD - 2х, тогда угол ABD - 3 х. Получем уравнение: 2х + 3х = 90° (так как угол В - прямой). 5х=90 х=18 Если х =18, тогда угол СBD(2x) = 18 * 2 = 36 (°), а угол ABD (3х) = 18 * 3 = 54(°). Проверим: Угол CBD + ABD = B, 36 град + 54 град = 90° (все верно) Так как диагонали в прямоугольнике равны, то равны ВО и СО, а значит треугольник ВОС - равнобедренный и угол ВОС = 36° (угол CBD = BOC). Угол ВОС = 180 - (36+36) = 108° Ответ: Угол ВОС = 108° Диагонали прямоугольника ABCD пересекаются в точке О. Найдите угол между диагоналями, если угол АВО равен 30 гр. Диагонали прямоугольника образуют четыре равнобедренных треугольника. Треугольнк АВО=треуг СОД, треуг СОВ=треуг АДО. Углы АОВ и СОД = 180-60=120°. углы (равные) СОВ и АОД =(360-240):2=60° АВО - р/б, тк ВО = АО( диагонали в прямоугольнике делятся точкой пересечения пополам + они равны) => угол АВО= углу ОАВ = 30 => угол АОВ = 180 - 60 = 120. Угол АВО=30, значит, угол ДВС=90-30=60 град Угол ВСА=ДВС по постороению=60 град угол ВОС=180-(60+60)=60 град угол АОД=ВОС=60 град Угол ВОА= 180-60=120 град Угол СОД=АОВ=120 град Так как угол ABO=30°, значит угол BAO=30°, исходя из этого угол BOA=180°-(30°+30°)=120° =>COD=BOA=120°, как вертикальный угол. В прямоугольнике углы сторон=90°, значит углы OBC=OCB=ODA=OAD=90°-30°=60°. Диагонали прямоугольника ABCD пересекаются в точке О. Найдите угол AOD, если ∠ABD - ∠СBD = 10°. Ответ дайте в градусах. 1) Так как АBCD - прямоугольник, то угол ABC = 90. Пусть угол CBD = x°, тогда угол ABD = x+10°, Всего 90°. Составим и решим уравнение: x+10+x=90 2x=80 x=40 Итак, угол CBD = 40°, а угол ABD = 40+10=50°. 2) Так как ABCD - прямоугольник, то DO=OА - по свойству диагонали в прямоугольнике. Отсуда следует, что треугольник АОD - равнобедренный по определению. Так как это равнобедренный треугольник, то углы ODA и OAD равны по свойству равнобедренного треугольника. Угол ODA=CBD - по свойству накрест лежащих углов (параллельные прямые AD и СB и секущая DB) Угол ODA=OAD=40°. 3) Проведем OE - перпендикуляр к AD. OE - высота, медиана треугольника ADO и биссектриса угла DOA. Треугольник EDO - прямоугольный. Если ODA = 40°, а DEO = 90°, то DOE = 180-90-40=50. Угол DEO = AOE, так как OE - биссектриса. Угол AOD = 50+50=100°. Ответ: 100°. Диагонали прямоугольника ABCD пересекаются в точке О, угол BCO=24°. Найти угол AOD Имеем прямоугольник ABCD. Диагонали AC и BD, которые пересекаются в точке O. Угол ABO=36°. Найти угол AOD. Т. К. диагонали прямоугольника равны и точкой пересечения делятся пополам, то треугольник ABO - равнобедренный. Значит, ABO=BAO=36.ABO+BAO+AOB=180°. Угол AOB= 180-( ABO+BAO). угол AOB=180 - (36+36)=108. Т. К. AOB+AOD=180(эти углы смежные), то AOD=180-108=72°. ИЛИ ТАК Сначала найдём угол AOB. Треугольник AOB - равнобедренный с основанием AB, углы ABO и BAO равны 36°. Угол AOB равен 180 - 2 * 36 = 108°. Угол AOD равен 180 - AOB = 180 - 108 = 72° Диагонали прямоугольника ABCD пересекаются в точке О. Найдите угол ABD если он на 30° больше угла COD Диагонали прямоугольника равны и в точке пересечения делятся пополам. Пусть угол СОД равен х°, тогда угол АОВ равен х°, потому что углы равны как вертикальные. В равнобедренном треугольнике угол АВО больше угла СОД на 30°, поэтому угол АВО+ углу ОАВ= (х+30) Сумма углов треугольника АВО равна 180°. Составляем уравнение х+(х+30)+(х+30)=180 3х+60=180 3х=180-60 3х=120 х=40 граудсов (х+30)=40+30=70° составляет угол АВД Диагонали прямоугольника ABCD пересекаются в точке О. Угол AOD=100°. Найдите углы треугольника AOB. BD=AC свойство диагоналей прямоугольника значит ВО=АО т.к. ВО=АО значит треугольник АОВ равнобедренный угол АВО=углу ВАО свойство углов при основаниии равнобедренного треугольника угол АОD и угол ВОА смежные значит AOD+ВОА=180° свойство смежных углов угол АОВ=180-100= 80 АВО+ВАО+АОВ=180 свойство углов треугольника АВО=ВАО=(180-80)/2=50 Диагонали прямоугольника ABCD пересекаются в точке О. Найдите углы треугольника COD если угол ABD=40° Треугольник ABD=треугольник ACD по первому признаку равенства треугольников так как сторона AB=CD по определению прямоугольника это две противоположные стороны прямоугольника, 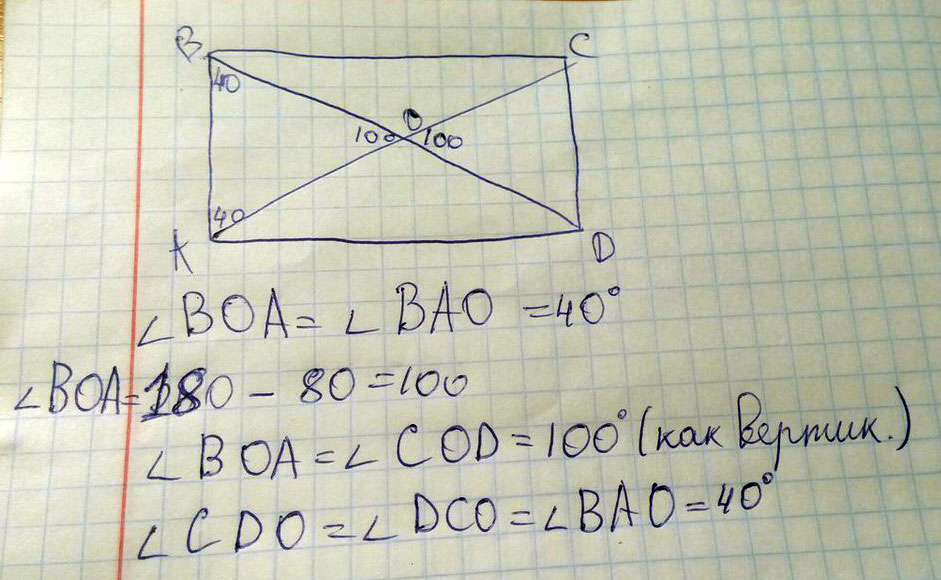сторона AD-Общая а угол BAD = углу ADC=90° по определению прямоугольника, у прямоугольника все углы равны 90°м следовательно треугольник ABD=треугольник ACD. тогда угол ABD = углу ACD = 40°м так как AB параллельна DC то угл ABD = углу BDC как накрест лежащие углы и рвны 40°м по условию тогда по определению сумма углов в треугольнике равна 180°м рассмотри треугольник COD углы COD+OCD+ODC=180гр 40+40 +углCOD=180 угл СOD =180-40-40=100°м ОТВЕТ угл COD=100гр. ; угл ODC=40гр ; угл OCD=40гр Диагонали прямоугольника ABCD пересекаются в точке О. Найдите угол AOB, если угол ODC=56° Рассмотрим треугольник AOB и треугольник EOD OB=OC (т.к. Диагонали прямоугольника равны) AO=OD AB=ED(т.к. Противоположные стороны равны) Значит треугольник AOB=EOD В равных треугольниках соответствующие элементы равны ⇒ угол ODC = углу OAB = 56°. Рассмотрим треугольник AOB - равнобедренный (т.к. Диагонали прямоугольника равны и точкой пересечения делятся пополам) В равнобедренном треугольнкие углы при основании равны, значит угол OAB= углу OBA = 56°. Сумма углов треугольника равна 180°, значит угол AOB = 180-56-56=68° Ответ:68° Диагонали прямоугольника ABCD пересекаются в точке О. Найти угол между диагоналями если угол BAC=50 Рассмотрим треугольник АВО. АО=ВО (т.к. По свойствам прямоугольника - диагонали его равны и точкой пересечения делятся пополам). Значит, треугольник АВО - равнобедренный и углы при его основании равны, т.е. ∠АВО=∠ВАО = 50°. Угол ∠ВОА (он же и есть острый угол между диагоналями) равен 180 - ∠АВО - ∠ВАО = 180 - 100 = 80°. Тупой угол между диагоналями определяем как (360-2*80)/2=100° Диагонали прямоугольника ABCD пересекаются в точке О. Найдите угол BDA если угол AOB равен 70 Рассмотрим треугольник АОВ. Сторона АО=ОВ (т.к. Диагонали прямоугольника точкой пересечения делятся пополам), значит, треугольник АОВ - равнобедренный и углы при основании равны (по свойствам равнобедренного треугольника). Значит, угол АВО = углу ВАО = (180 - 70)/2 = 55° Угол АВС = 90° т.к. АВСД - прямоугольник, значит, угол СВД = 90 - угол АВО = 90-55=35° По свойству параллельных прямых (в данном случае АД║ВС), накрест лежащие углы равны, т.е. угол СВД= углу ВДА = 35°