Найти площадь равнобедренного треугольника, если боковая сторона равна 20см, а угол при основании равен 30°.

Решение:
Проведем в этом треугольнике высоту. Т. к. эта высота лежит против угла в 30° то она равна 1/2 гипотенузы (боковой стороны) и равна 10. Расстояние от точки пересечения этой высоты до угла при основании находим по теореме Пифагора:  = √(20²-10²)=√300=10√3 полностью основание будет равно двум этим расстояниям: 20√3 Находим площадь как половину произведения основания на высоту: (1/2)*(10*(20√3))=100√3

Найти площадь равнобедренного треугольника, если его основание 8 см, а угол между боковыми сторонами равен 60°

Пускай дан треугольник АВС, АВ = АС, АС = 8. Угол В = 60°.
Также угол А = угол С, и А + В + С = 180°
Значит 2А = 120°, значит А = 60°
Треугольник равносторонний со стороной 8.
Площадь равностороннего треугольника равна \( \frac{\sqrt{3}*8^{2}}{4} = 16\sqrt{3} \)

Данный нам равнобедренный тр-к с углом между боковыми сторонами равным 60°°, является на самом деле равносторонним, так как на два равных угла при основании остается 180-60=120. То есть углы при основании также равны 60.
Площадь равностороннего тр-ка равна: S=(√3/4)*a² = (√3/4)*64 ≈ 27,7 cм²

Найти площадь равнобедренного треугольника, если основание равно 16 см, а боковая сторона 10 см.

1. S=1/2a*h=1/2*16*h=8*h.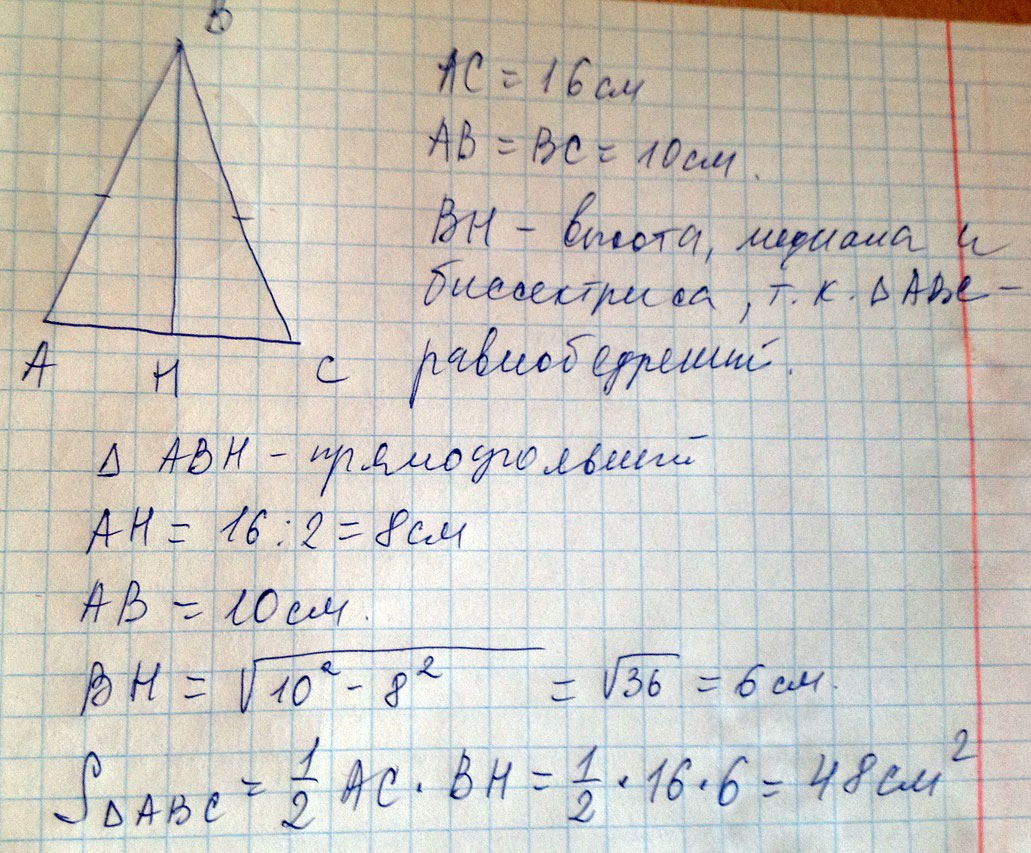
Задача свелась к нахождению высоты.
2. Проведем высоту ВН. Так как треугольник равнобедренный, то высота ВН является и медианой, следовательно, АН=НС=16:2=8 см.
3. Рассмотрим треугольник ABH. Он прямоугольный, АВ=10 см, АН=8 см. Найдем ВН по т. Пифагора.
ВН=квадратный корень из АВ в квадрате - АН в квадрате = квадратный корень из 100-64 = квадратный корень из 36 = 6 см.
ВН - это высота.
4. S=8*6=48 см^2
Ответ: S=48cм^2

Найти площадь равнобедренного треугольника, если боковая сторона равна 20см а угол при основании равен 30°

Sтреугольника = основание*высоту / 2
если провести в равнобедренном треугольнике высоту к основанию, получится прямоугольный треугольник с острым углом в 30°, катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы, значит высота будет равна 20/2 = 10.
осталось найти основание.
в равнобедренном треугольнике высота является и медианой, значит, если найти второй катет в получившемся прямоугольном треугольнике -то найдем половину основания.
по т. Пифагора второй катет = корень(20^2-10^2) = корень(300) = 10корень(3)
=> основание = 20корень(3)
Sтреугольника = 20корень(3) * 10 / 2 = 100корень(3)

Найти площадь равнобедренного треугольника, если его боковая сторона равняется 8 см, а угол при основе - 30°.

Проведем высоту из вершины.
Получим 2 маленьких треугольника.
Высота поделит основание на 2 равные части.
Высота равна половине стороны равнобедренного треугольника (как катет против угла в 30°)и равна 4 см.
Из маленького треугольника по теореме Пифагора найдем половинку стороны основания.
Она равна \( 6 \sqrt{3} \)
Значит основание равно \( 12 \sqrt{3} \).
Площадь равна:\( 0,5 * 4* 12 \sqrt{3} \) = \( 24 \sqrt{3} \)

Высота 4, так  как катет лежащий против угла 30° равен 0,5 гипотенузы. Из этого же прямоугольного треугольника находим половину основания через косинус острого угла в прямоугольном треугольнике. Получим 8√3/2, следовательно основание 8√3. Площадь0,5·8√3·4=16√3

Найти площадь равнобедренного треугольника, если высота, опущенная на основание, равна 10, а высота, опущенная на боковую сторону, равна 12.

Прямоугольные треугольники ВНС и АН1С подобны по первому признаку подобия: два угла одного треуг-ка соответственно равны двум углам другого. В нашем случае углы АН1С и ВНС прямые, а угол С - общий. Для подобных треугольников можно записать отношение сходственных сторон: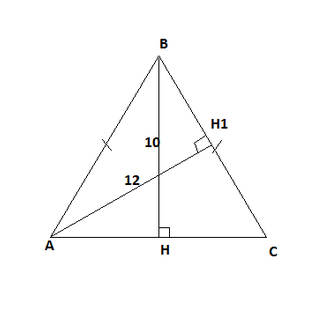
ВН: АН1=10:12, k=5/6, СН: СН1=5:6, отсюда
CH1=6CH:5
В прямоугольном треугольнике АН1С по теореме Пифагора находим АС:
АС²=AH1²+CH1²
Т. К. В равнобедренном треуг-ке АВС высота ВН, проведенная к основанию, является также и медианой, то СН=1/2АС, и выражение CH1=6CH:5 примет такой вид:
СН1=3АС:5.
Это значение для СH1 будем использовать в вычислении по теореме Пифагора:
АС²=12² + 9AC²/25
AC² - 9AC²/25=144
16AC²=3600
AC² = 225
AC=15 см
S ABC = 1/2AC*BH=7,5*10=75 см²

Найти площадь равнобедренного треугольника, если его основание равно 12 см, а угол лежащий на основании 45º.

Так как углы при основании 45° то в сумме они дают 90°, значит угол при вершине 90°, отсюда треугольник прямой. Проводим высоту из вершины. Так как треугольник равнобедренный то высота является и биссектрисой и медианой, значит она делит треугольник на 2 прямоугольных равнобедренных треугольника и делит основание пополам 12/2= 6 см
значит высота тоже равна 6
S = 1/2 bh
S = 1/2 * 6 * 12 = 36