Основой пирамиды является равнобедренный треугольник, у которого основания и высота равняется


Главная Научный калькулятор
Меню Алгебра Геометрия Основные понятия Аксиомы планиметрии Углы Перпендикулярные и параллельные прямые Перпендикуляр и наклонная Круг (окружность) Треугольник Четырехугольник Параллелограмм Трапеция Многоугольники Основные понятия стереометрии Аксиомы стереометрии Прямые в пространстве Пересекающиеся прямые Параллельные прямые Скрещивающиеся прямые Прямая и плоскость в пространстве Перпендикулярность прямой и плоскости Параллельность прямой и плоскости Угол между прямой и плоскостью Теорема о трех перпендикулярах Формула двойного проектирования Плоскости в пространстве Пересекающиеся плоскости Параллельность плоскостей Перпендикулярность плоскостей Площадь проекции плоской фигуры на плоскость Многогранники: Пирамида Призма Тела вращения: Цилиндр Конус Шар (Сфера) Объем тел вращения Задачи по геометрии Примеры решений Вспомогательные материалы: Таблицы Брадиса Исследование функций Асимптоты. Первая производная. Вторая производная. Тригонометрия Тригонометрические неравенства Преобразования графиков	Треугольник : Равнобедренный треугольник : Прямоугольный треугольник : Четырехугольник : Параллелограмм : Ромб : Прямоугольник : Трапеция : Многоугольники : Круг и окружность : Прямые и плоскости : Пирамида : Пространственная система координат : Цилиндр : Конус : Углы : Призма : Параллелепипед : Сфера и Шар Основой пирамиды является равнобедренный треугольник, у которого основания и высота равняется по 8см. Все боковые ребра наклонены к основанию под углом 45. Найдите боковое ребро Решение: Обозначим пирамиду АВСS. S вершина пирамиды. По условию основание АС=8 и высота ВК=8. Треугольник равнобедренный, значит АК=КС=8/2=4. Сторона треугольника основания АВ=корень из(ВК квадрат+АК квадрат)=корень из(64+16)=4 корня из 5=8,96. Из вершины пирамиды S опустим перпендикуляр на основание SO=H. Это высота пирамиды, а точка О центр вписанной в треугольник окружности, поскольку грани пирамиды имеют равный наклон. В равнобедренном треугольнике радиус вписанной окружности можно найти по известной формуле R=в/2корень из(2а-в)/(2a+b). Подставляем R=8/2корень из(28,96-8)/(28,96+8)=2,48. ОК=R=2,48. Высота пирамиды также равна Н=R=2,48. Поскольку треугольник SOK равнобедренный. Углы по 45°. АО=корень из(ОК квадрат +АК квадрат)=корень из(R квадрат+4 квадрат)=4,71. Тогда искомое боковое ребро AS=корень из(SOквадрат+АО квадрат)=корень из(2,48квадрат+4,71квадрат)=5,23. Основанием пирамиды является равнобедренный треугольник с углом 120°. Боковые рёбра образуют с её высотой, равной 16 см, углы в 45°. Найдите площадь основания пирамиды. Высота равноудалена от вершин треугольника. Потому, что все боковые ребра образуют с высотой одинаковые углы, и поэтому равны по длине. Это вообще касается любого отрезка из данной точки, имеющего заданный угол с перпендикуляром к плоскости, проходящим через эту точку. Иначе говоря, вершина пирамиды проектируется на центр описанной окружности. Причем раз нам задан угол (45°) и высота, то радиус описанной окружности равен высоте, то есть 16. Теперь нам надо сосчитать площадь равнобедренного треугольника с углом 120°, вписанного в окружность радиуса 16. Можно, конечно, сосчитать тупо все длины, а можно сообразить, что вместе с радиусами, проведенными в концы основания треугольник образует ромб, (как бы составленный из 2 равносторонних треугольников, хотя даже это не обязательно - можно просто сказать, что центральные углы сторон получаются по 60°). Поэтому боковые стороны треугольника равны 16, а площадь S = 1/2(16^2)sin(120) = 64корень(3) все ребра под углом 45 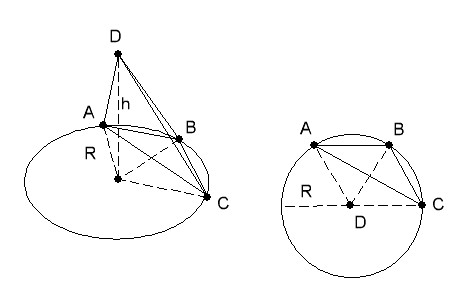все они проецируются на плоскость основания длина всех проекций одинакова и равна 16 * ctg(45)=16 вершина проецируется в центр описанной окружности радиус ее 16 теперь рассмотрим проекцию пирамиды на плоскость основания равнобедренный треугольник с углом 120, вписан в окружность радиуса 16 две меньших стороны такого треугольника равны радиусу, равны 16 площадь этого треугольника 1616sin(120)/2=1616корень(3)/4=64корень(3) В основании пирамиды лежит прямоугольный треугольник, один из катетов которого равен 6 см. Все боковые рёбра пирамиды равны 13 см. Высота пирамиды равна 12 см. Вычислить второй катет треугольника. Для того, чтобы ребра пирамиды, в основании которой лежит прямоугольный треугольник, могли быть равными, их проекции должны быть равными. Такое может быть только если основание высоты пирамиды находится в центре гипотенузы прямоугольного треугольника. Тогда два ребра имеют проекцию на гипотенузе, третье - медиане треугольника и все три наклонных и проекции оказываются равными. Задача из тех, что можно назвать удобными для решения: стороны рассматриваемых треугольников из числа Пифагоровых троек, т.е. стороны в которых образуют группу прямоугольных треугольников. По открытой еще древними математиками истине, данные числа удовлетворяют уравнению x² + y² = z² Таковы, например: x = 3, y = 4, z = 5 или x = 5, y = 12, z = 13 Таких троек немало. Вот несколько, которые полезно помнить. (3, 4, 5), (6, 8, 10), (5, 12, 13), (9, 12, 15) Вот и в этой задаче встречаются две таких тройки. Одна - высота пирамиды, половина основания и боковое ребро составляют тройку 12, 5 - катеты, 13 - гипотенуза. Поэтому без вычисления можно сказать, что гипотенуза основания равна 25. Что касается второго катета основания - гипотенуза равна 10, один катет 6, второй обязательно будет 8 см. Т.е. стороны основания отосятся как 3:4:5 (6:8:10) Ответ: Второй катет основания равен 8 см. Но можно пользоваться и теоремой Пифагора Рисунок очень простой. Нарисовать прямоугольный треугольник (так, чтобы он был похож на лежащий на плоскости). Из центра гипотенузы возвести высоту, соединить вершину с углами основания, нарисовать проекцию третьего ребра (медиана основания) Основанием пирамиды DABC является равнобедренный треугольник ABC, в котором стороны AB и AC равны, BC=6 см, высота AH равна 9см. Известно также, что DA=DB=DC=13см. Найдите высоту пирамиды В основании - равнобедренный треугольник с основанием 6 и высотой 9, боковая сторона равна √90. Его площадь равна 69/2 = 27. Радиус описанной вокруг него окружности равен произведению всех сторон, деленному на четыре площади: 690/(427) = 5. Так как боковое ребро равно 13 см, то высота пирамиды равна √13^2 - 5^2 = 12 Ответ: 12 см. Найдем боковые стороны равнобедренного треугольника по теореме Пифагора AC=AB = корень из ( AH^2+(1/2BC)^2) = корень из (90) Теперь найдем площадь этого треугольника S=1/2AHBC = 27 см^2 После находим радиус описанной окружности, через его площадь R = (ABACBC)/4S = 5 см и по теореме Пифагора находим высоту пирамиду DO = корень из ( AD^2 - R^2) = 12 см Ответ : 12 см Основанием пирамиды является равнобедренный треугольник с основанием 6см и боковым ребром 5см. Боковые грани пирамиды, которые содержат боковые стороны этого равнобедренного треугольника, перпендикулярны основанию, а 3-я боковая грань наклонена к плоскости основания под углом 60° Найдите высоту пирамиды Дана треугольная пирамида ABCD, в основании которой равнобедренный треугольник АВС (АВ=ВС=5, АС=6). Боковые грани пирамиды, содержащие стороны АВ и ВС, перпендикулярны основание, т. Е. DB - высота пирамиды. Проведем высоту (медиану и бисс-у) ВК треугольника АВС. Рассмотрим треугольник АКВ -прямоугольный. АК=АС/2=3, АВ=5 ВК^2 = AB^2- AK^2 BK = 4 Рассмотрим треугольник DBK - прямоугольный. Угол BKD=60 гр, следовательно, угол BDK=30 гр. Катет, лежащий напротив угла 30 гр, равен половине гипотенузы. BK=1/2DK DK=8 DB^2 = DK^2 - BK^2 DB = корень из 48 = 4 корня из 3 Основанием пирамиды DABC является равнобедренный треугольник ABC с гипотенузой АС=4√2. Ребро АD перпендикулярно плоскости АВС и равно 4. Отрезки АМ и АL являются соответственно высотами треугольников ADB и ADC. Найдите объем пирамиды AMLC. Пусть N- середина АС. Тогда BN перпендикулярно плоскости ADC, поскольку BN перпендикулярно АС (медиана равнобедренного треугольника) и AD (BN лежит в плоскости ABC). 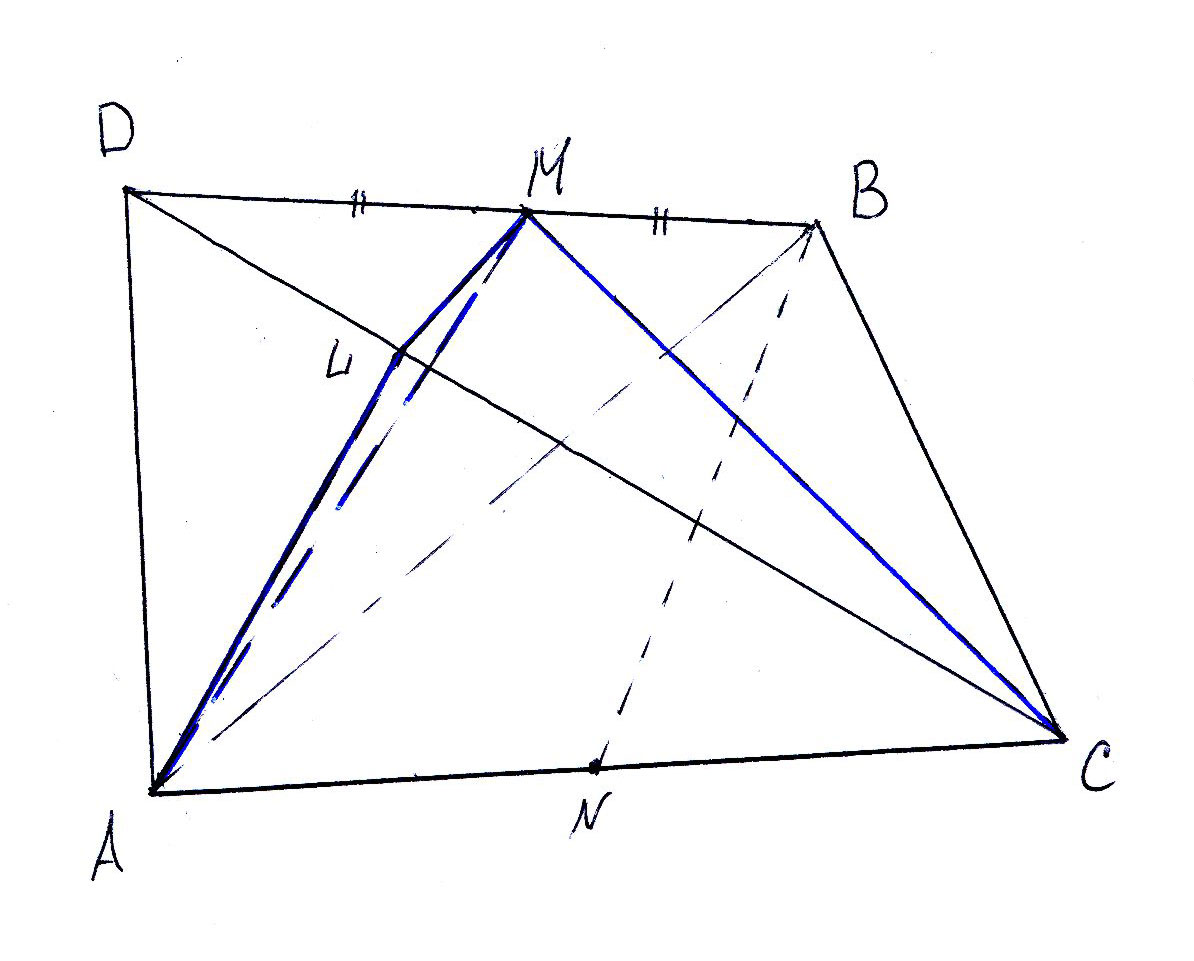BN = AC/2 = 2√2; это - расстояние от точки В до плоскости ADC. Поскольку точка М лежит на наклонной прямой DB посредине между D и B, расстояние от M до плоскости ADC равно h = BN/2 = √2; это можно считать высотой пирамиды ALCM, за основание принята грань ALC, осталось сосчитать её площадь. AL - высота в прямоугольном треугольнике ACD, где AD = 4; AC = 4√2; откуда DC = 4√3; AL = ADAC/DC = 4√(2/3); При этом из подобия ADC и ALC LC/AL = AC/AD = √2; LC = 8/√3; Площадь ALC равна S = LCAL/2 = 16√2/3; Объем ALCM равен V = Sh/3 = 32/9; Основанием пирамиды служит равнобедренный прямоугольный треугольник с катетом 6 см. Боковые ребра наклонены к плоскости основания под углом 30°. Найдите объем пирамиды Опустим высоту из вершины, обозначим вершины треугольника \( A,B,C \) а вершину пирамиды \( D \). Так как у нас треугольник одновременно равнобедренный, то, по теореме Пифагора: \( \sqrt{26^2}=6\sqrt{2} \). Проекция высоты, проведенной из вершины, будет радиусом описанной окружности около треугольника \( ABC \) Он равен половине гипотенузы, то есть \( R=3\sqrt{2} \). \( S=\frac{66}{2}=18 \) Тогда, проведя радиус, треугольник образованный между высотой и радиусом, получаем \( L=\frac{3\sqrt{2}}{sin60}\\ L=\frac{6\sqrt{2}}{\sqrt{3}}\\ H=\sqrt{36\frac{2}{3}-18} = \sqrt{6}\\ V=\frac{18\sqrt{6}}{3}=6\sqrt{6} \) Найти объем пирамиды, если основанием её является равнобедренный треугольник со сторонами 13, 13, 10 см. Каждое боковое ребро образует её высотой угол в 60°. Треугольники ASH, SBH и CSH равны по стороне и прилегающим углам 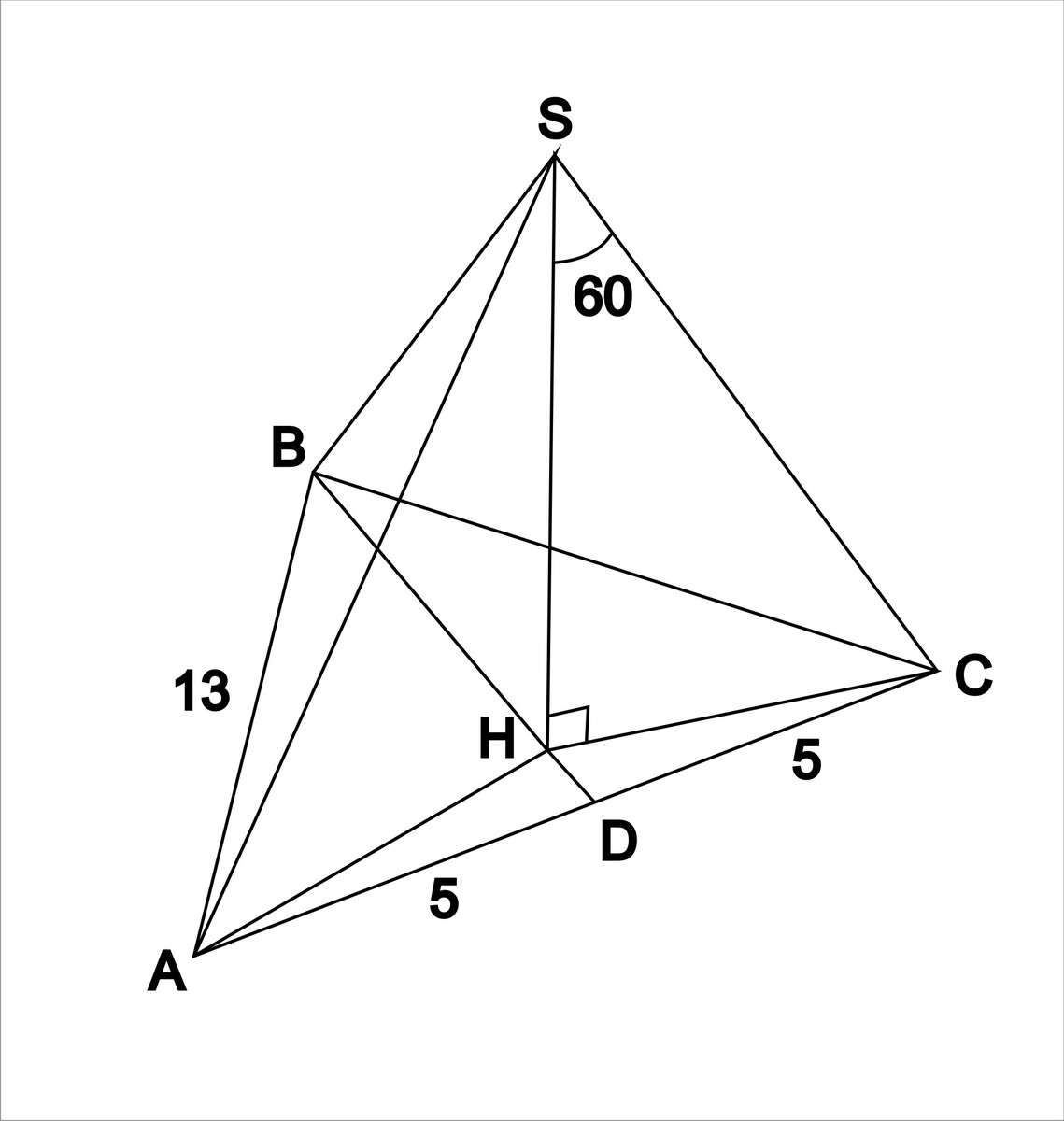SH-общая, прилегающие углы равны получается точка Н лежит в центре описанной около основания окружности R=(abc)/(4S)=(AB·BC·AC)/(4·BD·AD)=169/24=HC SH=HC·tg30=169/(24√3) V(пирамиды)=(1/3)H·S(основания)=(1/3)·HS·BD·AD=(845√3)/18 Основой пирамиды является равнобедренный треугольник с основанием 6 см и боковой стороной 5 см. Боковые грани пирамиды, содержащие боковые стороны этого равнобедренного треугольника, перпендикулярны к основанию, а третья боковая грань наклонена к плоскости основания под углом 60°. Найти высоту пирамиды. Дана треугольная пирамида ABCD, в основании которой равнобедренный треугольник АВС (АВ=ВС=5, АС=6). Боковые грани пирамиды, содержащие стороны АВ и ВС, перпендикулярны основание, т.е. DB - высота пирамиды. Проведем высоту (медиану и биссектрису) ВК треугольника АВС. Рассмотрим треугольник АКВ - прямоугольный. АК=АС/2=3, АВ=5ВК^2 = AB^2- AK^2BK = 4 Рассмотрим треугольник DBK - прямоугольный. Угол BKD=60 гр, следовательно, угол BDK=30 гр. Катет, лежащий напротив угла 30 гр, равен половине гипотенузы. BK=1/2DKDK=8 DB^2 = DK^2 - BK^2DB = корень из 48 = 4 корня из 3 Основанием пирамиды является равнобедренный треугольник с углом 120°. Боковые ребра образуют с ее высотой, равной 16, угол в 45°. Найдите V пирамиды. Если исходить из того, что ВСЕ боковые рёбра образуют угол в 45° с высотой, получится, что их проекции на основание будут также равны 16 (т.к. треугольник "высота"-"ребро"-"проекция ребра" получится равнобедренным прямоугольным). Теперь нарисуем основание и нанесём всё то, что нам известно: 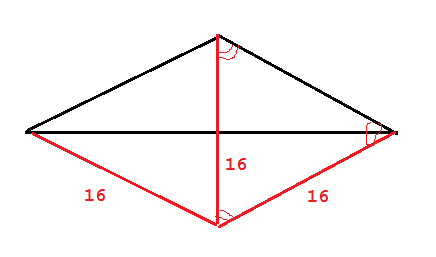1. Точка-проекция верхней точки пирамиды будет лежать на линии из тупого угла, являющейся медианой/биссектрисой/высотой треугольника-основания. 2. Точка-проекция верхней точки пирамиды равноудалена от всех вершин основания на 16. Это значит, что она лежит ВНЕ треугольника основания - т.е. сама пирамида как бы нависающая. Теперь рассмотрим треугольник, образованный боковой стороной основания, проекцией ребра из тупого угла и проекцией ребра из острого угла. Он равнобедренный, и один из углов при основании равен 120/2 = 60° - а значит он не просто равнобедренный, но и равносторонний. Боковая сторона основания, таким образом, равна 16. Дальше найдём "длинную" сторону основания - 2* 16cos (30) = 32 \( \sqrt{3} \)/2 = 16 \( \sqrt{3} \) А опущенная на неё из тупого угла высота: 16sin (30) =16 1/2 = 8 Площадь треугольника: 1/2 * a * h = 1/2 * 16 \( \sqrt{3} \) * 8 = 128 \( \sqrt{3} \) Объём пирамиды: 1/3 * 128 \( \sqrt{3} \) * 16 = 2048/3 * \( \sqrt{3} \) В основании пирамиды лежит равнобедренный прямоугольный треугольник. Боковая грань, проходящая через гипотенузу, перпендикулярна плоскости основания и является равнобедренным треугольником с боковой стороной 9корней из 3. Каждая из двух других боковых граней составляет с плоскостью основания угол, синус которого равен 4/корень из 17. Найдите объём пирамиды. АВС- прямоугольный равнобедренный треугольник. 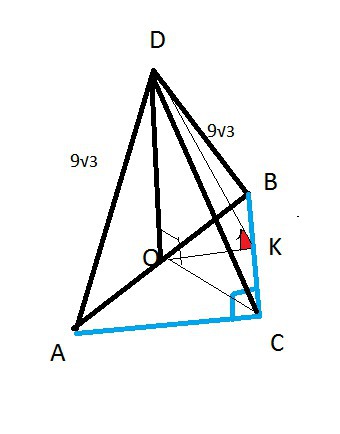Пусть АС=ВС=х, тогда АВ=х√2. МАВ- равнобедренный треугольник. МО- высота, медиана и биссектриса. АО=ОВ=x√2/2; ОК⊥ВС МК⊥ВС по теореме о трех перпендикулярах. sin∠MKO=4/√17 ⇒ cos∠MKO=1/√17⇒tg∠MKO=4. МО=ОК·tgMKO=(x/2)·4=2x По теореме Пифагора из прямоугольного треугольника МВО: МВ²=МО²+ОВ²; (9√3)²=(2х)²+(х√2/2)²; 243=9х²/2; х²=54 х=3√6 V=(1/3)·(AC·BC/2)·MO=(1/6)·(x·x/2)·2x=x³/6=(3√6)³/6=27√6. О т в е т. V=27√6.

Найти объем пирамиды, если основанием её является равнобедренный треугольник со сторонами 13, 13, 10 см. Каждое боковое ребро образует её высотой угол в 60°.

Основанием пирамиды является равнобедренный треугольник с углом 120°. Боковые ребра образуют с ее высотой, равной 16, угол в 45°. Найдите V пирамиды.