На гипотенузе AB прямоугольного треугольника ABC взята точка E, а внутри треугольника- точка D. Перпендикуляр EP к прямой AC делит катет АС пополам, угол В=45*, угол CDA= 90*, угол DCA=60*. Докажите, что EP=DC.

Решение:
так как EP перпендикулярно АС и ВС перпендикулярно АС, то ЕР=АР так как треугольники АРЕ и АВС подобны, DC это катет напротив угла в 30°, значит AC=2DC=2EP, EP=DC

Имеем РАВНОБЕДРЕННЫЙ ПРЯМОУГОЛЬНЫЙ треугольник. Отсюда понятно, что AD = DC = PE = BC/2 (ну, средняя линяя). Построим в нем окружность на стороне АС как на ДИАМЕТРЕ. Точка E САМО СОБОЙ лежит на этой окружности. Поскольку угол CDA прямой, то вершина ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА, ОПИРАЮЩЕГОСЯ НА ДИАМЕТР, лежит на окружности. Осталось только соединить D и P и заметить, что треугольник DPC - равнобедренный с углом 60° у основания СD, то есть РАВНОСТОРОННИЙ.  Поэтому CD = PD = PC = AP = PE .... и т.д.

На гипотенузе ВС прямоугольного треугольника АВС взята точка М. Высота МР треугольника АМС=4, высота MN треугольника АМВ=3. Найти АМ?

MP перпенд. AC, MN перпенд. АВ, угол А=90 гр. Угол NMP=90 гр. Четырехугольник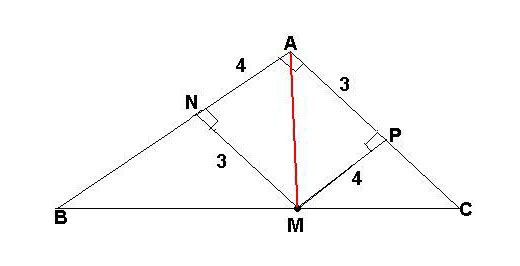
MNAP прямоугольник и АМ найдем по т. Пифагора АМ^2=4^2+3^2=25, AM=5
Можно уточнить доказательство вида четырехугольника.
АС перпенд. АВ, MN перпенд. АВ, значит MN параллельна АС(MN парал. АР), точно также МР парал. AN, значит MNAP параллелограмм, а так как у параллелограмма есть прямой угол, то это прямоугольник.

На гипотенузе АВ прямоугольного треугольника АВС взята точка Е, а внутри треугольника АВС взята точка D. ЕМ перпендикулярно АС, АМ=СМ, угол В равен 45 градусам, угол СDА равен 90 градусам, угол DСА равен 60 градусам. Доказать: ЕМ=DC

В прямоугольном треугольнике сумма острых углов равна 90. Если угол В равен 45, то угол А тоже 45.  В треугольнике ЕАМ угол м - прямой, угол А =  45, значит и угол Е=45.  Треугольник ЕАМ - равнобедренный, а в равнобедренном треугольнике боковые стороны равны. Значит ЕМ=АМ.
А в треугольнике АДС угол Д- прямой, угол С=60, значит угол САД равен 30. А в прямоугольном треугольнике катет, лежащий против угла в 30° равен половине гипотенузы. Значит, СД=1/2 АС. Но АМ=СМ =ЕМ =  1/2АС.
Отсюда, СД=ЕМ

---

Пусть АМ = СМ = а, тогда АС = 2а.
Если угол В = 45гр, то поскольку  ΔАВС прямоугольный, то второй уострый угол его угол А = 45гр. Тогда ΔАВС равнобедренный и ВС = АС = 2а.
Поскольку АМ = СМ, а ЕМ перпендикулярно АС, то ЕМ параллельно ВС и ЕМ - средняя линия ΔАВС и ЕМ = 0,5ВС = а
В ΔАСД  угол Д прямой, АС - гипотенуза, а угол АСД = 60гр. Следовательно угол САД = 30гр. А катет СД, лежащий против угла в 30 гр. Равен половине гипотенузы АС, т.е. СД = АС : 2 = а
Таким образом ЕМ = а и СД = а, т.е. ЕМ = СД, что и требовалось доказать.

На гипотенузе LM‍ прямоугольного треугольника LKM‍ лежит точка N.‍ На прямой LM‍ взята точка P‍ так, что точка M‍ находится между точками N‍ и P,‍ а угол NKP —‍ прямой. Найдите площадь треугольника NKM,‍ если известно, что ∠LKP = φ,‍ а площади треугольников LKM‍ и NKP‍ равны a‍ и b‍ соответственно.

Пусть ∠NKL = ∠MKP = φ - π/2 = α;
неизвестная площадь NKM = s;
a - s = KL*KN*sin(α)/2;
b - s = KM*KP*sin(α)/2;
если это перемножить, то
(a - s)*(b - s) = KL*KN*KM*KP*(sin(α))^2/4 = a*b*(sin(α))^2;
(a - s)*(b - s) = a*b*(sin(α))^2;
осталось решить квадратное уравнение
s^2 - (a + b)*s + a*b*(cos(α))^2 = 0;
s = (a + b)/2 +- √((a + b)^2 - a*b*(cos(α))^2);
s = (a + b)/2 +- √(a^2 + b^2)/2 + a*b*(sin(α))^2);
Осталось понять, какой оставить знак.
s = (a + b)/2 - √(a^2 + b^2)/2 + a*b*(cos(φ))^2);
я нашел частный случай, очень легкий, и по нему можно понять, что остается именно "минус". Пусть α = π/6; и сам треугольник KLM имеет угол L = π/6; оба треугольника получаются одинаковые, и их пересечение имеет площадь a/2, то есть s = (a + b)/4

В равнобедренном треугольнике ABC точки D и E взяты на основании AC так, что AD=CE. Из точек D и E к основанию проведены перпендикуляры до пересечения с боковыми сторонами треугольника соответственно с точкам M и N. Докажите, что DM=EN.

В ΔAMD и ΔCNE имеем:
∠D = ∠E = 90° (по построению),
∠A = ∠C (как углы при основании равнобедренного ΔABC),
AD = EC (по построению).
Следовательно, ΔAMD = ΔCNE, а значит DM = EN

Внутри треугольника АВС взята точка О, равноудаленная от его сторон. Найдите угол АОС, если угол АВО равен 39 гр.

Точка, равноудалённая от сторон треугольника является центром вписанной в него окружности. Он, в свою очередь, лежит на пересечении биссектрис треугольника, значит АО - биссектриса угла АВС.  ∠АВС=2∠АВО=2·39=78°.
В треугольнике АОС ∠ОАС+∠ОСА=(∠ВАС+∠ВСА)/2=(180-∠АВС)/2=(180-78)/2=51°.
∠АОС=180-(∠ОАС+∠ОСА)=180-51=129° - это ответ.
PS. Так как точка О не является центром описанной вокруг треугольника окружности, нельзя говорить о том, что угол АВС вписанный и, тем более, что угол АОС центральный и что он равен двум вписанным.