Правильная треугольная призма вписана в шар. Найдите высоту призмы если радиус шара √7/√3 см, а ребро основания призмы 2 см.

Решение:
так как центры вписанного и описанного шара совпадают..что намного облегчает решение задачи..мы найдем высоту: для начала..найдем радиус описанной окружности у основания: r = 2h/3 так как известны все стороны найдем h = √ 4 -1 = √3 r = 2√3/3 из треугольника (прямоугольного) который образуется если соединим радиусы и H/2. H/2 = √ 7/3 - 4/3 = √3/3 = √1 = 1 H = 2 см есть формула: R’’ = (H/2)" + r" R - радиус шара r  - радиус описанной окружности у основания призмы H - высота призмы

Правильная треугольная призма вписана в шар радиуса 8. Ребро основания призмы равно 5. Найдите высоту призмы

В призме АВСА₁В₁С₁ точки О₁ и О₂ - центры описанных около оснований окружностей.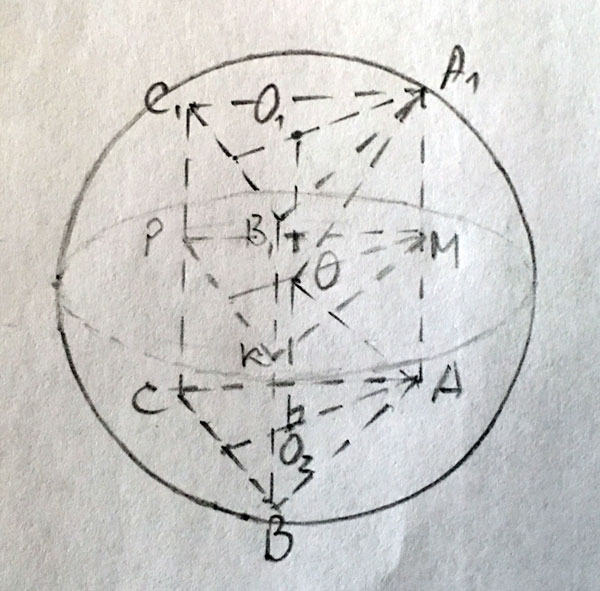
Для правильного треугольника радиус описанной окружности: Rо=a√3/3 ⇒ R=АО₂=А₁О₁=5/√3.
Точка О - центр шара.
Окружности, описанные около оснований призмы лежат на поверхности окружности.  
Плоскость РКМ проходит через середину высоты призмы и параллельна её основаниям.  ΔРКМ=ΔАВС.
Плоскости АВС и А₁В₁С₁ параллельны, и равноудалены от плоскости РКМ, значит плоскость РКМ пересекает поверхность шара по окружности, центр которой лежит на прямой О₁О₂. В точке О.  
В прямоугольном тр-ке AОО₂ АО=Rш=8, АО₂=Rо=5/√3.
ОО₂²=АО²-АО₂²=64-25/3=167/3.
h=О₁О₂=2·ОО₂=2√(167/3)≈14.9 - это ответ.