Найдите острые углы прямоугольного преугольника АВС, если высота ВD, проведённая к гипотенузе, отсекает от гипотенузы АС отрезок DC, равный 9см. ; ВС=6√3см.

Решение:
проекция катета ВС = 9 см, отсюда составим уравнение: проекция катета ВА = х вся гипотенуза 9+х, (9+х)*9 = 36*3 (т.е. ВС" = проекция катета ВС * на всю гипотенузу) х = 3 см cos a = 6√3 / 12 = √3/2 = 30°, 2-й острый угол равен = 60°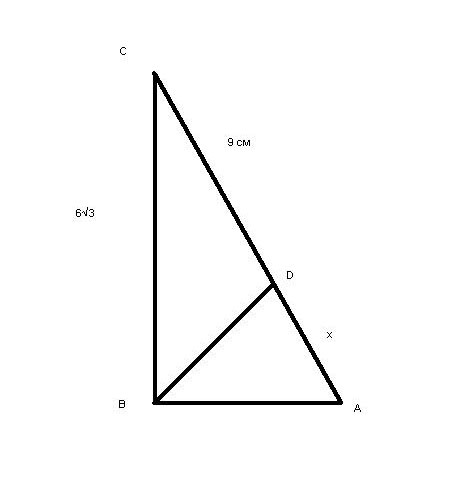

Найдите острые углы прямоугольного треугольника ,если его катеты равны 2,5 корней из 3-ех и 2,5 см

Есть треугольник, угол С = 90°. Найдем значение тангенса к одному из углов. Tga = противолежащий катет к прилежащиму. За противолежащий возьмём значение 2,5 а за прилежащий 2,5 корней из 3х. Значит 2,52,5корней из3х= сокращаем 2,5 получаем=1корень из 3х табличная величана угол в 30°. Остался другой острый угол: сумма углов треугольника составляет 180° значит: 180-90-30=60. Острые углы равны 60 и 30 грудусов

Найдите острые углы прямоугольного треугольника, если гипотенуза равна 7см, а один из катетов - 3,5корней из 3

Найдем еще один катет по теореме Пифагора 49-36,75=12,25 
Корень из 12,25=3,5
Найдем косинус острого угла 3,5/7=0,5 из этого следует то, что косинус 0.5 = 60°м. Следовательно Острые углы равны 30,60° т.к. В прямоугольном треугольнике один угол 90°, а сумма всех углов равна 180.
Ответ:30,60°

3) 3,5V3/7=V3/2 - это синус одного из острых углов. Значит угол равен 60°м, а второй - 30°м.