В ромбе острый угол равен альфа, а высота равна h. Найти длины диагоналей ромба

Решение:
в приложении первой строке следует читать L ADO=90-a/2 (по свойству ромба)

малая диагональ равна h/sin(П/2-a/2)=h/cos(a/2) d2=d1*ctg(a/2)=h/sin(a/2)

Дано: АBCD-ромб, BH-высота,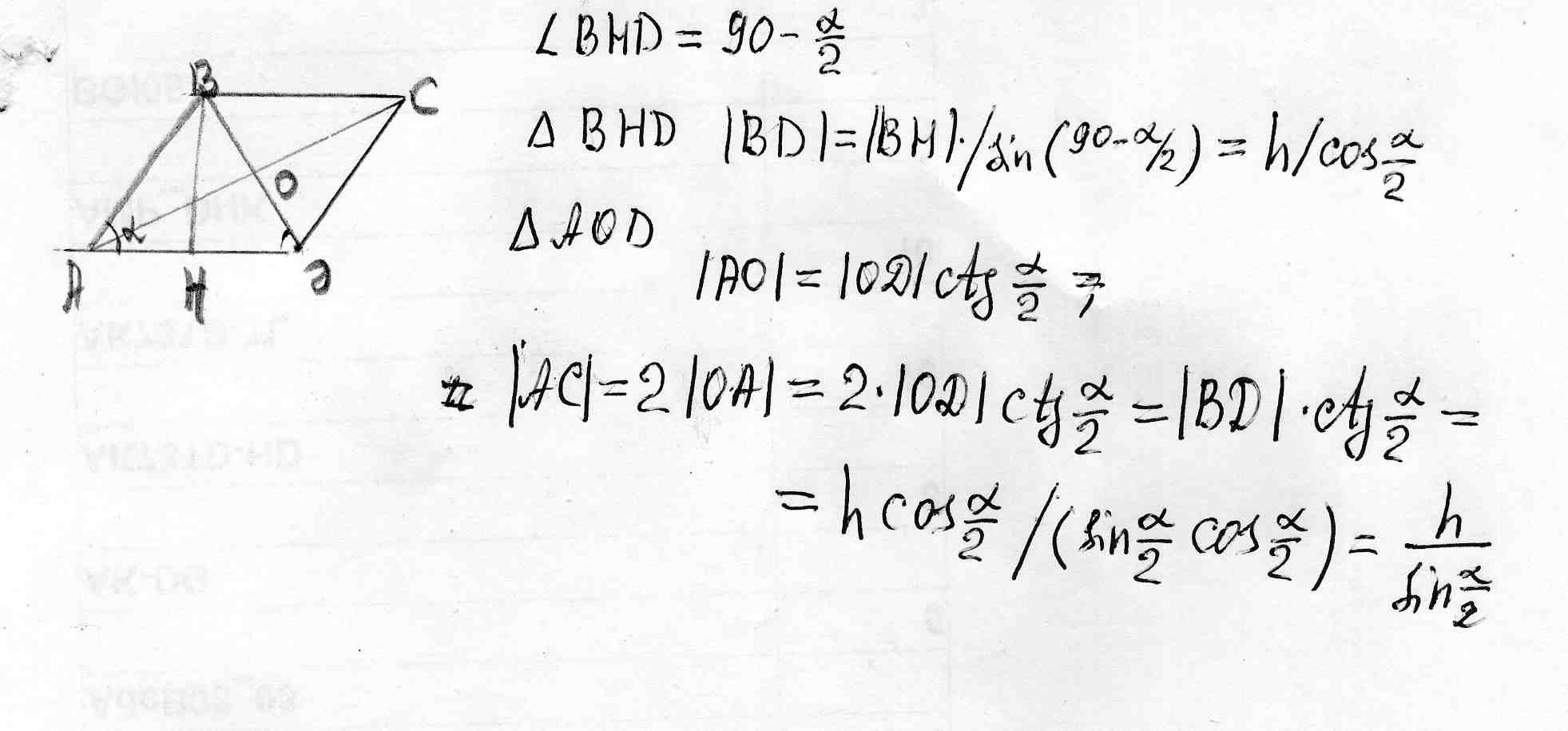

Острый угол ромба 60°, а его площадь 54корнеь3. Найти длину большей диагонали ромба

1. Площадь ромба \( S=54\sqrt3 \)
за формулой \( S=a^2sin\alpha, \) где \( \alpha \) - острый угол между сторонами ромба, найдем его сторону:
54\( 54\sqrt3=a^2sin60\\ \)

\( a^2=\frac{54\sqrt3}{sin60}\\ \)

\( a^2=\frac{54\sqrt3}{\frac{\sqrt3}{2}}={54\sqrt3}\cdot\frac{2}{\sqrt3}=54*2=108 \)

\( a=\sqrt{108}=4\sqrt7 \)
2.Диагонали ромба пересекаются под прямым углом, значит угол АОВ = 90°.
диагонали ромба также являются его бисектрисами.
т. О. Угол АВО=30.
значит треугольник АОВ - прямоугольный (угол АОВ=90) с острым углом АВО = 30.
и что следует с п. 1 стороной а=\( 4\sqrt7 \).
3. \( cosABO=\frac{BO}{AB} \)
\( BO=AB\cdot cos{ABO} \)\( BO=4\sqrt7 \cdot cos30 = 4\sqrt7 \cdot \frac{\sqrt3}{2}=2 \cdot \sqrt{21} \)

BD=2*BO

BD=2*\( BD=2\cdot BO= 2 \cdot 2 \sqrt{21} = 4 \sqrt{21} \)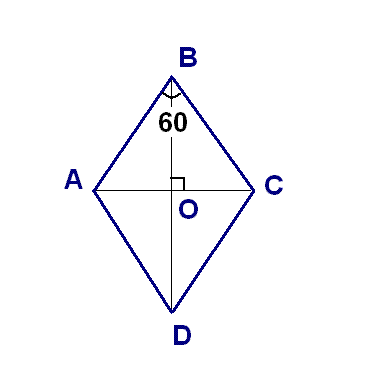

Перпендикуляр, проведенный из точки пересечения диагоналей ромба к его стороне, делит её на отрезки длиной 3см и 12см. Найти диагонали ромба.

Обозначим ромб АВСД. Проведём диагонали АС и ВД. Точка их пересечения О. Рассмотрим треугольник АВО. Проведём в нём высоту ОК на АВ. Тогда по условию ВК=3, АК=12. В прямоугольном треугольнике высота проведённая на гипотенузу делит его на подобные треугольники. Отсюда ВК/ОК=ОК/АК. Или 3/ОК=ОК/12. ОТсюда ОК=6. По теореме  Пифагора ВО=корень из(ВК квадрат+ОК квадрат) = корень из(9+36)=3 корня из 5. Отсюда диагональ ВД=2 ВО=6 корней из 5.  Из подобия треугольников ВОК и АОК получим АО/АК=ВО/ОК. Или АО/12=(3 корня из 5)/6. Отсюда АО=6 корней из 5. Тогда диагональ АС=2АО=12 корней из 5.

Периметр ромба равен 20см, а один из углов равен 60°. Найти длину диагонали, противолежащей этому углу.

Нарисуйте ромб, как параллелограмм, т.е. не вертикально, а так, что бы он опирался на одну из своих сторон, как принято рисовать параллелограмм. Обозначте его АВСД.
Тогда угол А равен 60°, Ав=АД=5(периметр 20, а все стороны равны, их четыре, значит каждая по 5)Получается треугольник АВД (ВД-это та самая наша диагональ, которая противолежит этому углу в 60 град). Но АВ=АД =5 и треугольник АВД равнобедренный, где диагональ ВД как бы основание. Тогда углы в равнобедренном треугольнике при основании равны. И если сумма всех углов 180° один из них 60° то на два других приходится 120° но они равны, значит на все углы этого треугольника приходится по 60° А такой треугольник называется равносторонним, следовательно и искомая диагональ, которая в ромбе, равна 5, как третья равная сторона в треугольнике АВД

Радиус вписанной окружности в ромб равен 8√3. А один из углов равен 2π/3, найти длину меньшей диагонали.

Если 1 угол равен 2п/3, то он равен 120°-это тупой угол ромба. Противолежащий ему также 120°. Значит, 2 другие угла по 60.
Получается, что меньшая диагональ делит ромб на 2 равносторонних треуг-ка и сторона ромба =меньшей диагонали d1.
Радиус вписанной в ромб окружности равен d1*d2/4a=8корней из 3, а т.к. Меньшая диагональ равна стороне, то подставляем d1 вместо а и получаем, что d2=32 корня из 3.
Рассмотрим прямоугольный треугольник, образованный половинами диагоналей и стороной ромба: по т. Пифагора находим сторону :
(Корень из a^2-a^2/4)=(1/2)*16 корней из 3.
Находим сторону а =32 и значит меньшая диагональ равна 32.

Острый угол ромба EFPT равен 60°. Его периметр 48 см, найти длину меньшей диагонали данного ромба.

Сторона ромба равна периметр, деленный на 4 = 12 (стороны ромба равны)
В прямоугольном треугольнике, образованном половиной диагонали ромба и стороной, прилегающей к углу 60°, один угол равен 30° и против этого угла лежит половина меньшей диагонали. (все это потому что диагонали ромба перпендикулярны и являются биссектрисами).
Итак, половина меньшей диагонали равна половине стороны = 6см.
Значит диагональ равна 12см

Одна из диагоналей ромба 12см, его площадь- 42 см в квадрате. Найти другую диагональ.

\( S=\frac{1}{2}*d_1d_2=42 \), где d1 и d2 - диагонали. Подставляем известную диагональ в это формулу площади. \( 42=\frac{1}{2}*12*d_2 \), откуда \( d_2=\frac{2*42}{12}=7 \)

Одна сторона ромба = 13, одна из диагоналей = 10, найти вторую диагональ

Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон. Т.к. в ромбе все стороны равны, то
d²+D²=4a²
100+D²=4*169
D²=676-100
D=√576
D=24

Диагонали ромба делит его на 2 равносторонних треугольника, радиус вписанной в него окружности равен 1, найти площадь и длины диагоналей

Дан ромб АВСД, диагональ Ас делит его на два равных треугольника АВСД и АДС, в равносторонний треугольник АВС вписана окружность, по формуле радиус вписанной в правильный треугольник окружности равен: а/2корня; где а- сторона ромба. Откуда, а=2корня3, т.к. Радиус равен1. Т. К. Треугольник равносторонний, то АС-диагональ, равна 2корня из 3 Проведем высоту ВН, получается прямоугольный треугольник по теореме Пифагора ВН=корень из АВ квадрат-АН квадрат=корень из 12-3=3. Т. К. Ромб-частный случай параллелограмма, то его диагонали точкой пересечения делятся пополам, значит диагональ ВД=6. Площадь ромба равна произведение диагоналей напополам, т.е. 6корней из 3

Сторона ромба равна 20, а острый угол равен 60°. Найти длину меньшей диагонали.

Нужно провести 2 высоты в ромбе, получится 4 маленьких треугольника. Нужно рассмотреть какой нибудь 1 треугольник, они все одинаковые.
в треугольнике имеем гипотенузу = 20 и угол в 30°( высота в равнобедренном треугольнике является биссектрисой). Найдем половину длины меньшей диагонали:
sin 30° = 1/2 =>
половина диагонали = гипотенузу × sin 30° = 20× 1/2 = 10
значит, диагональ = 10×2 = 20