В треугольнике АВС угол С=90, АС=8 см, sin A = 3/5. Найти длину гипотенузу треугольника.

Решение:
В моем решении воспользуемся теоремой Пифагора: AC=8 sinA=35=CBAB Получается что отношение CBAB к равно 35 но их длины могут быть и другие И для вычисления их длины нужно умножить на икс 3x5x=CBAB Теперь СB=3x AB=5x Составим соотношение 64=25х^2-9х^2 64=25х^2-9х^2 64=16х^2 4=x^2 x=2 И гипотенуза равна 5*2=10. Ответ 10

Биссектриса прямого угла и одного из острых углов треугольника образуют угол 105* найти гипотенузу треугольника если его меньший катет равен 2 см

АВС - прям. Тр-ик. С = 90 гр. АС = 2. СК и АМ- биссектрисы. О - т. Пересечения биссектрис. Угол АОС = 105 гр.   АВ = ?
В тр-ке АОС: угол АОС = 105 гр,  угол АСО = 45 гр (т.к. СК - биссектриса прямого угла).
Тогда угол ОАС = 180 - 105 - 45 = 30 гр.   Угол А = 60 гр. Угол В = 30 гр.
По свойству угла в 30 гр. В прям. Тр-ке АВС: АВ = 2*АС = 4 см.
Ответ: 4 см.

Один из катетов прямоугольного треугольника равен 5 см, а гипотенуза больше другого катета на 1 см. Найти гипотенузу треугольника.

Обозначим катет, который надо найти за x. Теперь по теореме Пифагора составляем уравнение
5^2+x^2=(x+1)^2
25+x^2=x^2+2x+1
2x=24
x=12
Ответ:12 см

Один из углов прямоугольного треугольника равен 60, а сумма гипотенузы и меньшего из катетов равна 26,4 см. Найти гипотенузу треугольника.

Пусть x - гипотенуза.
Меньший катет лежит против меньшего угла (он будет равен 90-60=30°).
Катет, лежащий против угла 30°, равен половине гипотенузы; значит меньший катет равен 0,5x.
Из условия следует: x+0,5x=26,4
1,5x=26,4
x=17,6 см
Ответ: 17,6 см
или так
Т. К. Это прямоугольный треугольник то углы его будут равны 60°, 90 и 30. Меньший катет лежит напротив угла в 30°. По правилу он равен половине гипотенузы. Поэтому задачу можно решить через уравнение. Пусть х - это катет, тогда гипотенуза равна 2х, а их сумма по условию равна 26,4 см. Составим уравнение.
х+2х = 26,4
3х= 26,4
х = 8,8
1. 8,8 * 2 = 17,6 см
Ответ 17,6 см.

Катет прямоугольного треугольника больше другого катета на 10 см, и меньше гипотенузы на 10 см, найти гипотенузу треугольника

Обозначим этот катет за х, тогда второй катет равен х-10, а гипотенуза х+10.
По теореме Пифагора
(х-10)²+х² = (х+10)²
-х²+40х=0
дальше через дискриминант
D=1600
√D=40
x1= -40-40/-2 = 40
x2= нет
Тогда наш катет равен 40, а гипотенуза 50.

в прямоугольном треугольнике АБС с гипотенузой АС, внешний угол при вершине А=120 градусам ; АБ=5 см. Найти гипотенузу треугольника.

угол A 180-120=60
угол B 180-90-60=30
теперь ABC - половина равностороннего.
AB = 5
а гипотенуза 5*2=10

Катеты прямоугольного треугольника относятся как 3:4, а разность длин их проекций на гипотенузу равна 7 дм. Найти гипотенузу треугольника.

Треугольник АВС, уголС=90, СН-высота на АВ, ВС/АС=3/4, АН-НВ=7
НВ=х, АН=х+7
СН= корень(НВ*АН)=корень (х в квадрате + 7х)
треугольники АНС и СНВ подобны по двум углам, уголВ=уголАСН, уголА=уголВСН
ВС/АС=НВ/СН, 3/4=х/ корень (х в квадрате + 7х), возводим обе части в квадрат
9/16 = х в квадрате/ (х в квадрате+7х)
16*х в квадрате =9*х вквадрате + 63х
х=9 =НВ, АН=9+7=16, АВ=16+9=25

В прямоугольном треугольнике медианы катетов равны корень 52 и корень73. Найти гипотенузу треугольника

Свойство медиан
медиана а в квадрате + медиана б в квадрате = 5 медиан с в квадрате
52+73=5 медиан с в квадрате
125=5медиан в кв
25= медиана с в квадрате                 медиана с =5
гипотенуза равна  двум  медианам следовательно гипотенуза равна  5*2=10 Ответ 10

Гипотенуза будет равна 10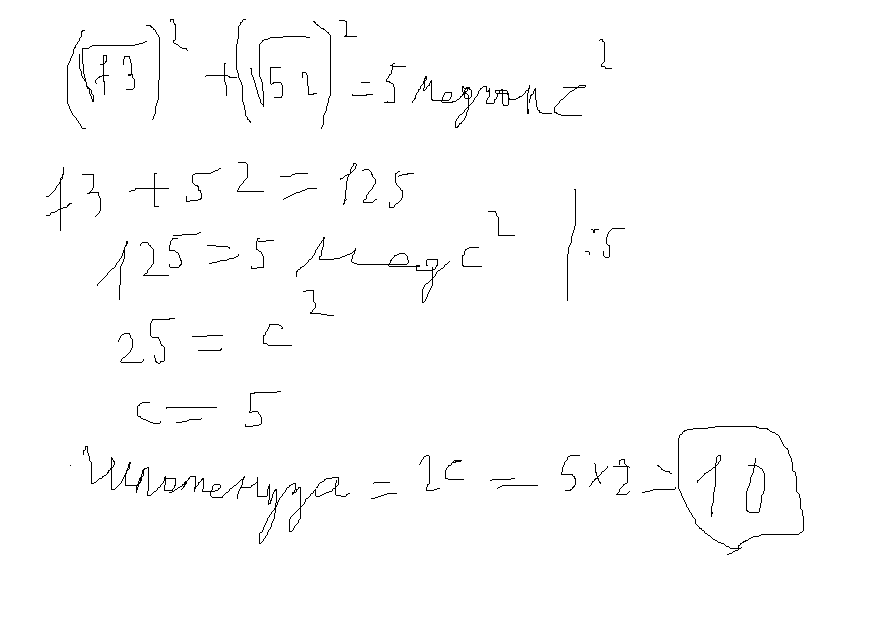

Катет прямоугольного треугольника равен 8 см а медиана проведённая к другому катету равна √ 73 см найти гипотенузу треугольника

1. В треугольнике АВС проведена медиана ВО
АВ=8см, ВО=V73 (V - знак корня)
В получившемся треугольнике АВО ВО является гипотенузой. По теореме Пифагора найдем катет Ао
(V73)^2=64+a^2
73=64+a^2
a^2=9
a=3
2. Т. К. Медиана делит сторону пополам, то АО=ОС, а АС=3+3=6
3. По теореме Пифагора найдем гипотенузу треугольника АВС
с^2=8^2+6^2=64+36=100
c=10
Ответ: гипотенуза = 10см