окружность радиуса 6 см касается внешним образом второй окружности в точке


Главная Научный калькулятор
Меню Алгебра Геометрия Основные понятия Аксиомы планиметрии Углы Перпендикулярные и параллельные прямые Перпендикуляр и наклонная Круг (окружность) Треугольник Четырехугольник Параллелограмм Трапеция Многоугольники Основные понятия стереометрии Аксиомы стереометрии Прямые в пространстве Пересекающиеся прямые Параллельные прямые Скрещивающиеся прямые Прямая и плоскость в пространстве Перпендикулярность прямой и плоскости Параллельность прямой и плоскости Угол между прямой и плоскостью Теорема о трех перпендикулярах Формула двойного проектирования Плоскости в пространстве Пересекающиеся плоскости Параллельность плоскостей Перпендикулярность плоскостей Площадь проекции плоской фигуры на плоскость Многогранники: Пирамида Призма Тела вращения: Цилиндр Конус Шар (Сфера) Объем тел вращения Задачи по геометрии Примеры решений Вспомогательные материалы: Таблицы Брадиса Исследование функций Асимптоты. Первая производная. Вторая производная. Тригонометрия Тригонометрические неравенства Преобразования графиков	Треугольник : Равнобедренный треугольник : Прямоугольный треугольник : Четырехугольник : Параллелограмм : Ромб : Прямоугольник : Трапеция : Многоугольники : Круг и окружность : Прямые и плоскости : Пирамида : Пространственная система координат : Цилиндр : Конус : Углы : Призма : Параллелепипед : Сфера и Шар Окружность радиуса 6 см касается внешним образом второй окружности в точке С. Прямая, проходящая через точку С, пересекает первую окружность в точке А, а вторую окружность-в точке В. Найти радиус второй окружности, если АС=4 см, ВС=6 см. Решение: Если провести касательную к обеим окружностям в точке С, то равенство вертикальных углов при этой касательной и заданной секущей АВ означает, что дуги обеих окружностей (АС и ВС) "имеют одинаковую градусную меру", то есть соответствующие им центральные углы равны. Это означает, что треугольники, образованные радиусами и хордами АС и ВС, подобны, то есть длина хорды пропорциональна радиусу, то есть ВС в полтора раза больше АС. Отсюда ответ - 9. Из центров окружностей О1 и О2 опустим перпендикуляры О1К1 и О2К2 на АВ. СК1 = АС/2 = 2; СК2 = ВС/2 = 3; О1К1 II О2К2 (обе прямые перпендикулярны АВ). Прямоугольные треугольники СО1К1 и СО2К2 подобны (у них все углы равны попарно). О2С/О1С = СК2/СК1; О2С/6 = 3/2; О2С = 9. Между прочим, заодно доказано, что углы АО1С и ВО2С, и прямые АО1 II ВО2; О₁ и О₂ - центры двух касающихся внешним образом окружностей. Прямая О1О2 пересекает первую окружность (с центром в точке О₁) в точке А. Найдите диаметр второй окружности, если радиус первой равен 5 см, а касательная, проведенная из точки А ко второй окружности, образует с прямой О₁О₂ угол в 30. Рисуем две касающиеся окружности: левая (меньшая) О₁ и правая (большая) О₂. Проводим прямую через точки О₁ и О₂. Крайняя левая точка пересечения с окр О₁ пометим как А. Проводим из точки А касательную АВ к окр. О₂. В - точка касания. Рассмотрим прям. Тр-ик АВО₂. В нем: АО₂ = 2R1 + R2 = 10 + R2, (гипотенуза). О₂В = R2 - катет против угла в 30 гр. 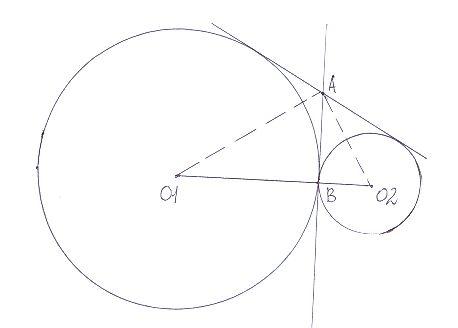Значит 2R2 = 10 + R2 R2 = 10, 2R2 = 20 Ответ: 20* Окружность радиуса 4 касается внешним образом второй окружности в точке. Общая касательная к этим окружностям, проходящая через точку В, пересекается с некоторой другой их общей касательной в точке. Найдите радиус второй окружности, если АВ=6. Решение очень простое - вся "хитрость" в том, что угол О1АО2 (между пунктирными прямыми) равен 90°м. Дело в том, что О1А и О2А - биссеткриссы смежных углов (почему биссектрисы, это понятно? Обоснуйте), а сумма смежных углов 180°. Ну, сумма половин смежных углов (то есть сумма угла О1АВ и угла О2АВ) дает 90. Таким образом, трегольник О1АО2 - прямоугольный, и АВ - высота к гипотенузе. Дальше - очень полезное "заклинание" - хотя и очень простое. Высота к гипотенузе делит прямоугольный треугольник на два, подобные ему - и между собой тоже, конечно. Поэтому О1B/АВ = АВ/О2В; О1B = АВ^2/O2B = 6^2/4 = 9; Две окружности касаются внешним образом в точке А. Прямая l касается первой окружности в точке В, а второй – в точке С. А) Докажите, что треугольник АВС прямоугольный. Б) Найдите площадь треугольника АВС, если радиусы окружностей 8 и 2 Из центров окружностей и точки А проведем перпендикуляры к прямой ВС отрезок общей внешней касательной к 2 окружностям равен 2VRr=2V16=8 обозначим точку пересечения перпендикуляра из т А с ВС точкой К ВК=КА=КС по свойству касательных проведенных из одной точки треугольникиВАК и КАС равнгобедренные и прямоугольные ВА=АС=√16+16=4√2 ВС гипотенуза =√32+32=8 значит треугольник АВС прямоугольный S=4√2x4√2/2=16ед² 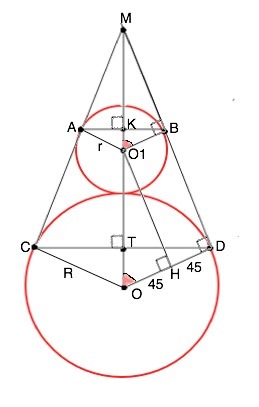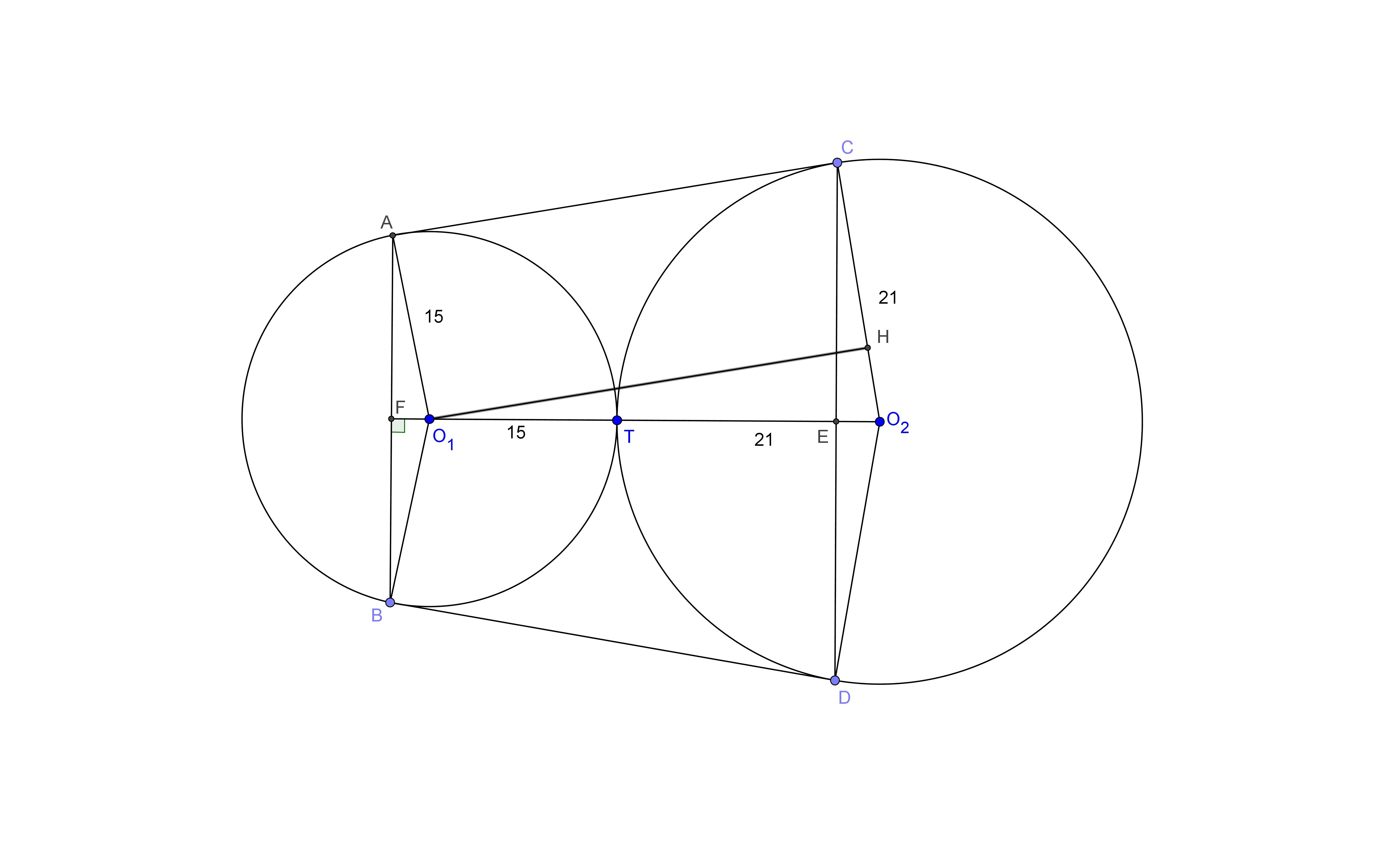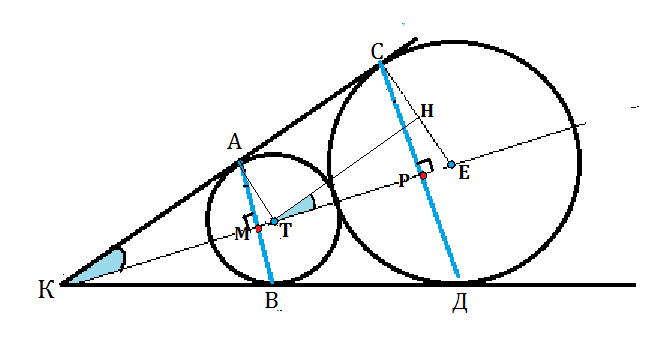Окружности радиусов 15 и 21 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD. Пусть О₁ и О₂ - центры меньшей и большей окружностей соответственно, а также пусть О₁O₂ пересекает AB и CD в точках F и Е (см. Рисунок). Опустим перпендикуляр O₁H на радиус O₂C. Тогда CH=AO₁=15 и cos(∠O₁O₂H)=O₂H/O₁O₂=(21-15)/(21+15)=1/6. Т. К. AO₁\|\|CO₂ (они перпендикулярны AC), то ∠AO₁F=∠CO₂E=∠O₁O₂H. Поэтому FO₁=AO₁cos(∠AO₁F)=151/6=5/2, O₂E=CO₂cos(∠CO₂E)=211/6=7/2. Отсюда искомое расстояние EF=FO₁+O₁O₂-O₂E=5/2+(15+21)-7/2=35. 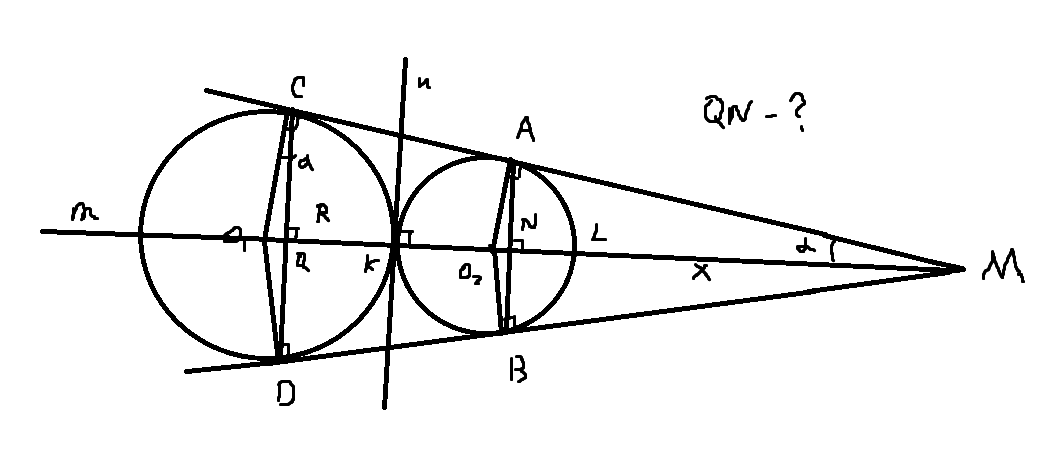Окружности радиусов 27 и 54 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD. R≡54,r≡27. Пусть # синвол параллельности, ↓ перпендикуляр. R ↓ ac, r ↓ ac ⇒ao2 # co1. (ao2=r, co1=R). o1,o2 ∈ m. Где m=Mo1 и M точка пересечение ac и bd. O1q ↓ cd, O2n ↓ ab. cd # ab. ( cd # n, n↓m ab # n). Значит qn расстояние между ab и cd. Угл cmo2=a ⇒ sin(a)=27/(27+x)=O2n/27 27/(27+x)=54/(108+x). Где x =LM L точка пересечение (o2;r) c m. Sin(a)=O1q/54=O2n/27. Отсюда O2n=9 O1q=18 ⇒ QK=54-18=36. QN= 36+27+9=72. Простите если непонятно писал. Обозначим центр меньшей окружности Т, большей - Е, точку соединения касательных АС и ВД - К. Соединим центры окружностей и точки касания с АC. Углы КАТ=КCЕ=90º Из Т проведем параллельно АC прямую до пересечения с радиусом CЕ в точке Н. CН=АТ НЕ=СЕ- CН=27. ТЕ=r+R=27+54=81 Косинус угла НЕТ=НЕ: ТЕ=27:81=1/3 Синус угла НЕТ=√(1-cos²∠НЕТ)=(2√2):3 ТН=ТЕsin TEH=81(2√2):3=54√2 В треугольнике КCЕ отрезок ТН паралллеьна и =АС - средняя линия. КC=2 ТН=108√2 КА=АC=54√2 КА=КВ, КС=КД как отрезки касательных из одной точки. Треугольники КАВ и КСД равнобедренные. КМ и КР - их высоты. АВ\|\| СД Треугольники КАМ и НЕТ подобны - прямоугольные и имеют равный острый угол. ⇒ угол МАК=углу НЕТ и их синусы равны. 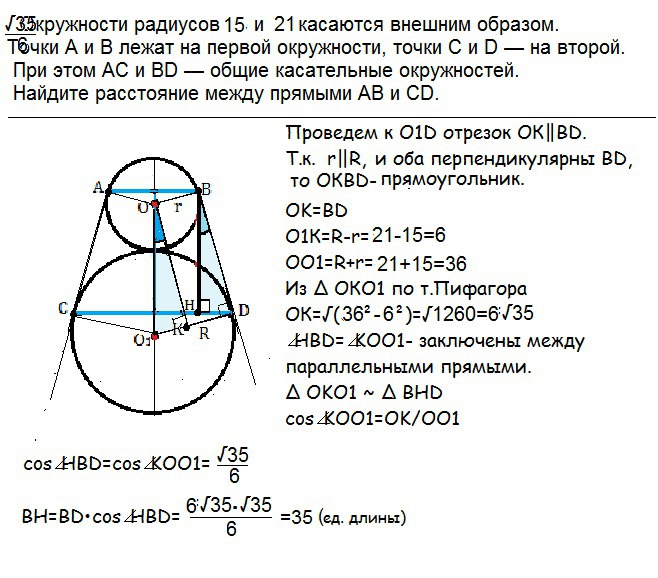КМ=АКsin∠МАК=(54√2)(2√2):3=72 АМ \|\| СР АМ - средняя линия треугольника СКР МР=КМ=72 и является расстоянием между АВ и СД Окружности радиусов 15 и 21 касаются внешним образом. Точеи А и В лежат на первой окружности, точки С и Д на второй. При этом АС и ВД общие касательные окружностей. Найдите расстояние между прямыми АВ и СД Искомое расстояние - длина перпендикуляра ВН, опущенного из В на СD. AB и CD - хорды, перпендикулярны прямой ОО1, содержащей диаметры окружностей. AB\|\|CD Пусть центр меньшей окружности - О, большей - О1. Проведем радиусы r и R в точки касания. Проведем к О1D отрезок ОК\|\|BD. Т. К. r\|\|R, и оба перпендикулярны ВD, то ОКВD- прямоугольник. ОK=BD О1К=R-r=21-15=6 OO1=R+r=21+15=36 Из ∆ OКО1 по т. Пифагора OК=√(36²-6²)=√1260=6√35 ∠HBD=∠KOO1- их стороны взаимно параллельны. ∆ OKO1 ~ ∆ BHD cos∠KOO1=OK/OO1 cos∠HBD=cos∠KOO1=(√35):6 BH=BD•cos∠HBD=(6√35)•(√35):6=35 (ед. Длины) это искомое расстояние. 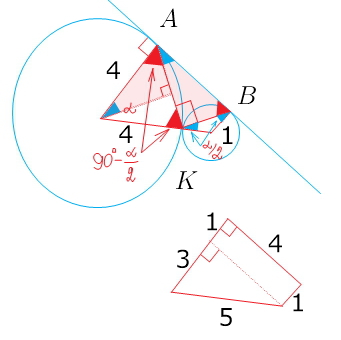Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй- в точке B. Найдите площадь треугольника AKB, если известно, что радиусы окружности равны 4 и 1. Первое, - треугольник АВК прямоугольный. Площадь прямоугольного треугольника = половине произведения катетов) гипотенуза АВ = 4 -это очевидно из получившейся трапеции. а чтобы найти катеты не хватает известных углов) на рисунке есть два равных треугольника: треугольник АВК равен половине равнобедренного треугольника с боковыми сторонами 4 -по гипотенузе и острому углу) из этого очевидно: АК = 2КВ по т. 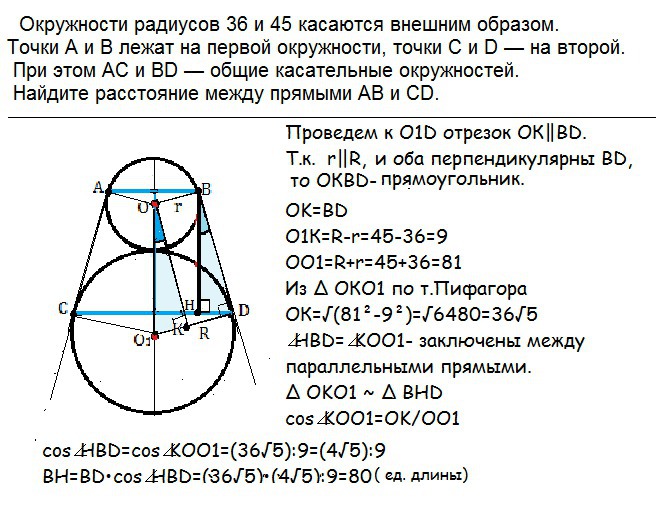Пифагора 4х² + х² = 16 -> 5x² = 16 S(ABK) = (1/2)x2x = x² = 16/5 = 3.2 Окружности радиусов 36 и 45 касаются внешним образом. Точки А и В лежат на первой окружности, точки С и Д- на второй. При этом Ас и ВД-общие касательные окружностей. Найдите расстояние между прямыми АВ и СД. Расстояние между центрами О1 и О2 окружностей равно 36+45 = 81. Из центра меньшей окружности проведём отрезок параллельно касательной до радиуса в точку касания большей окружности. Синус угла между этим отрезком и линией О1О2 равен (45-36)/81 = 9/81 = 1/9. Этот угол равен углам между АВ и СД и радиусами в точки касания. Тогда искомое расстояние L между АВ и СД равно: L = 81-45(1/9)+36(1/9) = 81-5+4 = 80. Искомое расстояние - длина перпендикуляра ВН, опущенного из В на СD. AB и CD - хорды, перпендикулярны прямой ОО1, содержащей диаметры окружностей. AB\|\|CD Пусть центр меньшей окружности - О, большей - О₁. Проведем радиусы r и R в точки касания. Проведем к О₁D отрезок ОК\|\|BD. Т. К. r \|\|R, и оба перпендикулярны ВD, то ОКВD- прямоугольник. ОK=BD О₁К=R-r=45-36=9 OO₁=R+r=45+36=81 Из ∆ OКО₁ по т. Пифагора OК=√(81²-9²)=√6480=36√5 ∠HBD=∠KOO₁- заключены между взаимно параллельными сторонами. ∆ OKO₁ ~ ∆ BHD cos∠KOO₁=OK/OO₁ cos∠HBD=cos∠KOO₁=(36√5):9=(4√5):9 BH=BD•cos∠HBD=(36√5)•(4√5):9=80 (ед. Длины) Окружности радиусов 4 и 60 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D - на второй. При это AC и BD - общие касательные окружностей. Найдите расстояние между прямыми AB и CD АО1=4, СО2=60, Найти АР. О1О2=4+60=64. АК=О1О2=64. АК║O1O2, АК⊥СД. Тр-ки АСК и CHR подобны, так как ∠К - общий и оба прямоугольные, значит АК/СК=СК/РК ⇒ РК=СК²/АК. КО2=АО1. СК=СО2-КО2=60-4=56. РК=56²/64=49. АР=АК-РК=64-49=15 - это ответ. 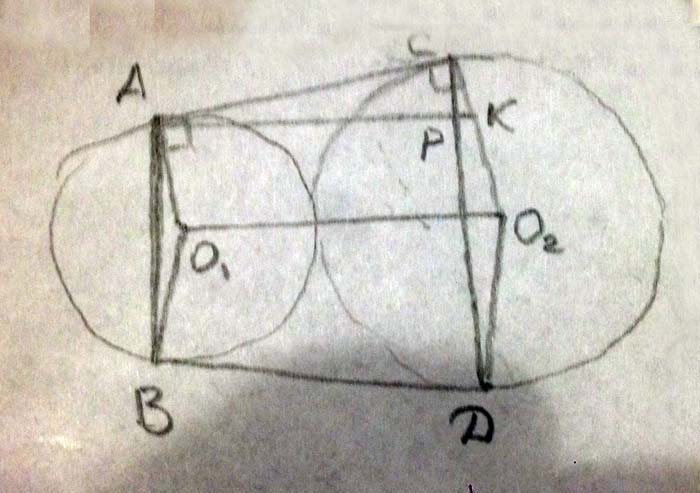Окружности радиусов 22 и 99 касаются внешним образом. Точки А и В лежат на первой окружности, точки С и В — на второй. При этом АС и BD — общие касательные окружностей. Найдите расстояние между прямыми АВ и CD Касательные АС и ВД образуют угол, биссектриса которого проходит через центры окружностей О1О2. Половина этого угла α равна углу между радиусами R1и R2, проведенными в точку касания и прямыми АВ и СД. Проведём отрезок из точки касания меньшей окружности параллельно О1О2 до прямой СД. sinα = (R2-R1)/(R2+R1)= (99-22)/(99+22) = 7/11 ≈ 0,636364. Расстояние от середины АВ до R1 равно 22(7/11) = 14. Расстояние от середины СД до R2 равно 99(7/11) = 63. Ответ: расстояние между прямыми АВ и CD равно (22+99)+14-63 = 72. 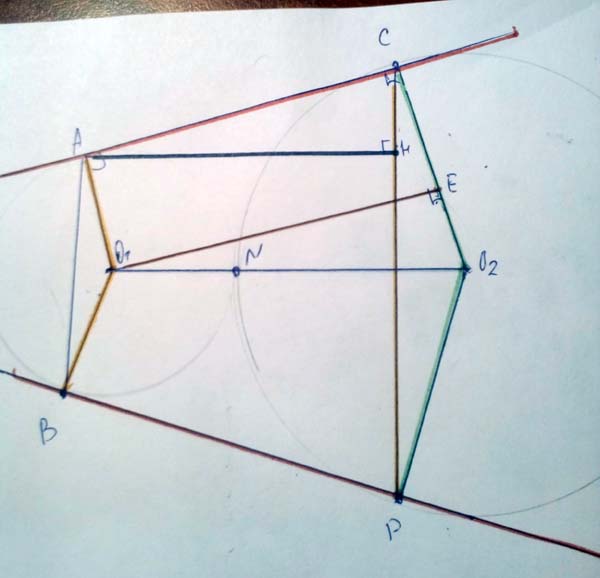Окружности радиусов 12 и 20 касаются внешним образом. Точки А и В лежат на первой окружности, точки С и D — на второй. При этом АС и BD — общие касательные окружностей. Найдите расстояние между прямыми АВ и CD. Дано: ω(O1; R1) ω(O2; R2) ω(О1;R1)∩ω(O2;R2) = N AC, BD - общие касательные A∈ω (O1;R1) B∈ω(O1; R1) C∈ω (O2;R2) D∈ω(O2; R2) R1 = 12 R2 = 20 AH⊥CD - AH - Решение: Пусть O1E⊥CO2. Тогда AO1CE - прямоугольник, т.к. ∠O1AC = ∠ACO1 = ∠O1EC = 90°. Тогда AC = O1E - как противоположные стороны прямоугольника. O1O2 = R1 + R2. CE = AO1 - опять же, к. AO1EC - прямоугольник. Тогда CE = R2 - AO1 = R2 - R1. По теореме Пифагора в ∆O1EC: O1E = √O1O2² - EO2² = √(R1 + R2)² - (R2 - R1)² = √R1² + 2R1R2 + R2² - R2² + 2R1R2 - R1² = √4R1R2 = 2√R1R2. ∠ACH =1/2UCD - как угол между касательной и хордой. ∠O1O2C = UNC = 1/2UCD (т.к. UNC = UND) - как центральный угол. Тогда ∠O1O2C = ∠ACD => sinACD = sinO1O2C. sinO1O2C = O1E/O1O2 = 2√R1R2/(R1 + R2) => sinACD = 2√R1R2/(R1 + R2). sinACD = AH/AC => AH = sinACD•AC = 2√R1R2•2√R1R2/(R1 + R2) = 4R1R2/(R1 + R2) Подставляем значения R1 и R2: AH = 4•12•20/(12 + 20) = 960/32= 30. Ответ: 30. 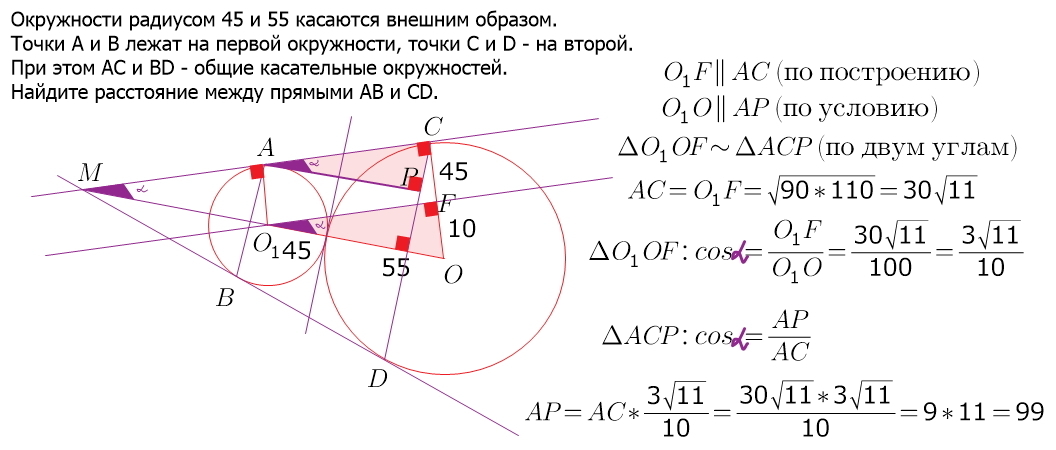Окружности радиусом 45 и 55 касаются внешним образом. Точки a и b лежат на первой окружности, точки c и d - на второй. При этом ِac и bd - общие касательные окружностей. Найдите расстояние между прямыми ab и cd. Касательные пересекутся в точке (обозначим) M центры окружностей (вписанных в угол между касательными) лежат на биссектрисе этого угла радиусы, проведенные в точки касания, перпендикулярны касательным) биссектриса будет и высотой и медианой в равнобедренных треугольниках CMD (AMB) т.к. Отрезки касательных, проведенные из одной точки, равны) получили подобные прямоугольные треугольники. Искомое расстояние = 99 Окружности радиусов 45 и 90 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D на второй. При этом AC и BD – общие касательные окружностей. Найдите расстояние между прямыми AB и CD. Продлим касательные до их пересечения в точке М. Центры О и О₁ касающихся окружностей лежат на биссектрисе МО угла СМD. r =O₁B=45, R=OD=90. Радиусы О₁В и ОD, проведенные в точки касания, перпендикулярны касательной МD (свойство радиусов). Из О₁ проведем О₁Н ║ МD. В параллелограмме О₁ВDО ∠В=∠D= 90°, следовательно, О₁ОDВ - прямоугольник. HD=O₁B, ОН=90-45=45. Прямоугольные ∆ МО₁В и ∆ МОD подобны по общему острому углу при М. ОО₁=R+r=90+45=135* *Косинус* равных углов при О и О₁=ОН/ОО₁=45/135=1/3. Тогда КО₁=О₁В•cos KO₁B=45•1/3=15 TO=DO•cos TOD=90•1/3=30 Расстояние между АВ и СD равно КТ=ОО₁-ТО+КО₁=135-30+15=120 (ед. Длины)