Основание пирамиды - прямоугольник со сторонами 6 и 8 см, каждое боковое ребро пирамиды - 13см. Вычислите высоту пирамиды.

Решение:
сначала можно найти диагональ(d) пирамиды по теореме Пифагора.d=sqrt{6^2+8^2}=sqrt{36+64}=sqrt{100}=10см.высота опущенная из вершины делит эту диагональ пополам. Значит ее половина равна 5см.теперь половина диагонали боковое ребро и высота образуют также прямоугольный треугольник. Найдем высоту(H) по теореме Пифагора.Н=sqrt{боковое ребро^2-половина диагонали^2}=sqrt{13^2-5^2}=sqrt{169-25}=sqrt{144}=12см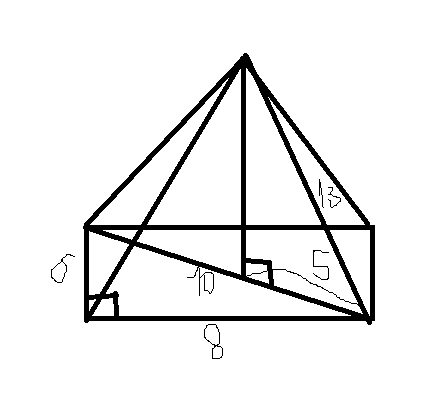

---

Так как SA = SB = SC = SD, то прямоугольные треугольники ASO, BSO, CSO и DSO равны по гипотенузе и общему катету SO.
Тогда AO = BO = CO = DO, а значит, точка О является точкой пересечения AC и BD. В ΔABD: BD = корень из (AB^2+AD^2) = корень из (6^2+8^2) = 10 см. Тогда ОВ = 1/2ВD = 5см.  в ΔSOD по теореме Пифагора: SO = корень из ( SD^2 - OD^2) = корень из ( 13^2 - 15^2) = 12 см. Ответ: 12 см.  
Рисунок сам построишь)

Высоту найдем из прямоугольного треугольника, образованного половиной длины стороны основания (катет), апофемой грани с основанием 6 см( гипотенуза), и самой высоты (второй катет)
Апофему найдем по теореме Пифагора из треугольника, образованного ребром пирамиды и половиной меньшей стороны основания
Апофема = √(13²-3²)=4√10.
Высота пирамиды равна корню из разности квадрата апофемы и квадрата половины от 8 и равна
√( 100-16)=√144=12 см

---

Pассмотрим одну из граней пирамиды - SBC. Проведем перпендикуляр SH к ВС, так как треугольник равнобедренный Н - середина ВС.
ВН = ВС/2 = 3.
SH = √(SC² - BH²) = √(169 - 9) = √160 = 4√10/
OH = АВ/2 = 4
искомая высота - SO = √(SH² - OH²) = √(160 - 16) = √144 = 12.
Ответ: 12.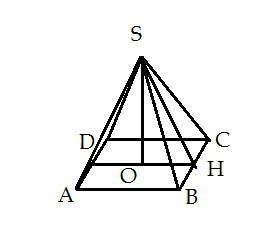